Уроки 63 - 73
§3.2. Алгебра логики

Содержание урока

3.2.1. Логическое умножение, сложение и отрицание

3.2.2. Логические выражения

3.2.3. Логические функции

Логические функции

Логическое следование (импликация)

Практическое задание «Функция импликации»

Логическое равенство (эквивалентность)

Практическое задание «Функция эквивалентности»

Контрольные вопросы. Задания. Компьютерный практикум

3.2.4. Логические законы и правила преобразования логических выражений

3.2.5. Решение логических задач

3.2.3. Логические функции

Логические функции

Любое логическое выражение можно рассматривать как логическую функцию F(X₁, Х₂,... Х_n), аргументами которой являются логические переменные X₁, Х₂,... Х_n. Сама функция и аргументы могут принимать только два различных значения: «истина» (1) и «ложь» (0).

Каждая логическая функция двух аргументов имеет четыре возможных значения. Каждое значение функции несет 1 бит информации, так как может быть либо 0, либо 1. Следовательно, каждая функция несет 4 бита информации и по формуле (2.1) можно определить, какое количество различных логических функций двух аргументов может существовать:

N = 2^I = 2⁴ = 16.

Таким образом, существует 16 различных логических функций двух аргументов, каждая из которых задается собственной таблицей истинности (табл. 3.8).

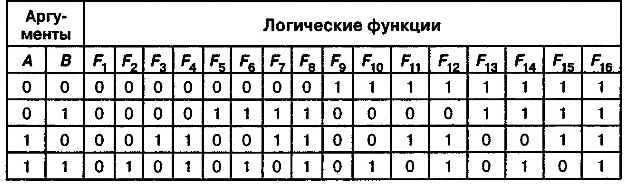
Таблица 3.8. Таблицы истинности логических функций двух аргументов

Легко заметить, что логическая функция F₂ является функцией логического умножения, F₈ — функцией логического сложения, F₁₃ — функцией логического отрицания для аргумента А и F_n — функцией логического отрицания для аргумента В.

В обыденной и научной речи кроме базовых логических связок «и», «или», «не» используются и некоторые другие: «если... то ...», «тогда... и только тогда, когда ...» и др. Некоторые из них имеют свое название и свой символ, и им соответствуют определенные логические функции.

Следующая страница Логическое следование (импликация)

Cкачать материалы урока