Урок 62
§36. Сложность вычислений
(§36. Сложность вычислений)

Содержание урока

Что такое сложность вычислений?

Примеры

Что такое асимптотическая сложность?

Алгоритмы поиска

Алгоритмы сортировки

Вопросы и задания

Задачи

Примеры

Рассмотрим алгоритмы выполнения различных операций с массивом А длины n, который может быть объявлен в программе на школьном алгоритмическом языке как

целтаб А[1:n]

Пример 1. Требуется вычислить сумму первых трёх элементов массива (при n ≥ 3).

Решение этой задачи содержит всего один оператор:

Sum:=А[1]+А[2]+А[3]

Этот алгоритм включает две операции сложения и одну операцию записи значения в память, поэтому его сложность Т(n) = 3 не зависит от размера массива вообще.

Пример 2. Требуется вычислить сумму всех элементов массива. В этой задаче уже не обойтись без цикла:

Sum:=0

нц для i от 1 до n

Sum:=Sum+A[i]

кц

Здесь выполняется п операций сложения и n + 1 операций записи в память ¹, поэтому его сложность Т(n) = 2n + 1 возрастает линейно с увеличением длины массива ².

---

¹ Здесь и далее для упрощения выводов мы не учитываем команды, необходимые для организации цикла, потому что при больших п время их выполнения очень мало в сравнении со временем выполнения остальных операторов.

² Предполагается, что сложение любых двух чисел выполняется одинаковое время.

---

Пример 3. Требуется отсортировать все элементы массива по возрастанию методом выбора.

Напомним, что метод выбора предполагает поиск на каждом шаге минимального из оставшихся неупорядоченных значений (здесь i, j, nMin и с — целочисленные переменные):

нц для i от 1 до n-1

nMin:=i;

нц для j от i+1 до n

если A[j]<A[nMin] то nMin:=j все

КЦ

если nMin<>i то

c:=A[i]; A[i]:=A[nMin]; A[nMin]:=с

все

кц

Подсчитаем отдельно количество сравнений Т_с(n) и количество перестановок Т_р(n). Количество сравнений не зависит от данных и определяется числом шагов внутреннего цикла:

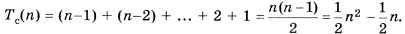
Число перестановок зависит от данных. Например, если массив уже отсортирован в нужном порядке, перестановок не будет вообще. В худшем случае на каждом шаге основного цикла происходит перестановка, всего их будет Т_р(n) = n - 1.

Следующая страница Что такое асимптотическая сложность?

Cкачать материалы урока