Урок 62
§36. Сложность вычислений
(§36. Сложность вычислений)
Содержание урока
Что такое сложность вычислений?
Что такое асимптотическая сложность?
Алгоритмы сортировки
Алгоритмы сортировки
Ранее мы проанализировали один из простых методов сортировки массивов — метод прямого выбора и выяснили, что его асимптотическая сложность O(n2). Повторим анализ для метода пузырька, который также изучался в 10 классе:

На первом шаге основного цикла выполняется n-1 шагов внутреннего цикла, т. е. n - 1 сравнений. Далее количество сравнений уменьшается до 1, так что общее количество сравнений равно:
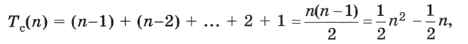
так же как и у алгоритма прямого выбора. В то же время в худшем случае при каждом сравнении выполняется перестановка, что требует
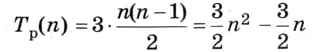
операций присваивания. Таким образом, этот алгоритм имеет асимптотическую сложность O(n2) как по числу сравнений, так и по числу присваиваний.
Существуют ли более эффективные сортировки, имеющие, например, линейную сложность? Да, для некоторых особых случаев существуют. Например, если известно, что все значения исходного массива находятся в интервале от 1 до некоторого значения МАХ, можно использовать сортировку подсчётом. Для этого выделяется дополнительный массив счётчиков:
целтаб С[1:МАХ]
который предварительно обнуляется:
нц для i от 1 до МАХ
С[i]:= О
кц
Затем в цикле проходим весь массив с данными и для каждого элемента A[i] увеличиваем счётчик С[А[i]]. Например, если А[i]=20, счётчик С[20] увеличивается на 1. После окончания цикла в каждом счётчике C[i] находится количество значений исходного массива, равных i.
нц для i от 1 до n
С [А [i]]:=С[A[i]]+1
кц
Теперь остаётся расставить числа в массиве А в нужном количестве. Например, если С[20] = 5, в массив А записываются последовательно 5 значений, равных 20:
k:= 1
нц для i от 1 до МАХ
нц для j от 1 до C[i]
А[к]:=i
к:=к+1
кц
кц
Попробуем подсчитать количество операций для этого алгоритма. Заполнение массива С нулями требует МАХ присваиваний. Цикл подсчёта элементов содержит п сложений и присваиваний, т. е. его сложность — линейная, O(n). Наконец, последний вложенный цикл выполняет также п сложений и присваиваний (по числу элементов массива А), поэтому алгоритм в целом имеет линейную сложность по n.
Однако нужно учитывать, что принципиальное ускорение алгоритма в сравнении с предыдущими получено за счёт того, что:
• все значения — целые числа в ограниченном диапазоне;
• есть возможность использовать дополнительный массив размером МАХ, который может значительно превышать размер исходного массива.
Здесь проявляется компромисс «скорость — память», который присутствует во многих задачах: ускорение алгоритма возможно за счёт использования дополнительной памяти и наоборот, экономия памяти приводит к замедлению работы алгоритма.
Доказано, что в общем случае вычислительная сложность сортировки, основанной только на использовании операций «сравнить» и «переставить», не может быть меньше, чем O(nlogn). Именно такую сложность имеют, например, сортировка слиянием (англ. merge sort) и пирамидальная сортировка (англ. heap sort), которые применяются при работе с большими наборами данных. Быстрая сортировка (англ. quick sort), которая изучалась в 10 классе, в среднем тоже имеет сложность O(nlogn), однако в худшем случае (когда на каждом шаге массив делится на две части, одна из которых состоит из одного элемента) требуется O(n2) обменов.
Следующая страница  Вопросы и задания
Вопросы и задания

