Урок 62
§36. Сложность вычислений
(§36. Сложность вычислений)

Содержание урока

Что такое сложность вычислений?

Примеры

Что такое асимптотическая сложность?

Алгоритмы поиска

Алгоритмы сортировки

Вопросы и задания

Задачи

Что такое асимптотическая сложность?

Допустим, что нужно выбрать между несколькими алгоритмами, которые имеют разную сложность. Какой из них лучше (работает быстрее)? Оказывается, для этого необходимо знать размер массива данных, которые нужно обрабатывать. Сравним, например, три алгоритма, сложность которых

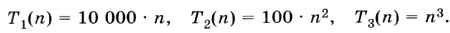
Построим эти зависимости на графике (рис. 5.8). При n ≤ 100 получаем Т₃(n) < Т₂(n) < Т₁(n), при n = 100 количество операций для всех трёх алгоритмов совпадает, а при больших n имеем Т₃(n) > Т₂(n) > Т₁(n).

Обычно в теоретической информатике при сравнении алгоритмов используется их асимптотическая сложность, т. е. скорость роста количества операций при больших значениях n.

При этом запись О(n) (читается «О большое от n») обозначает, что, начиная с некоторого значения n = n₀, количество операций ограничено функцией с • n, где с — некоторая константа:

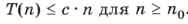
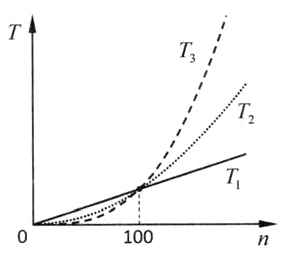
Рис. 5.8

Такие алгоритмы имеют линейную сложность, т. е. при увеличении размера данных в 10 раз объём вычислений увеличивается тоже примерно в 10 раз.

Пусть, например, Т(n) = 2n - 1, как в алгоритме поиска суммы элементов массива. Очевидно, что при этом Т(n) ≤ 2n для всех га ≥ 1, поэтому алгоритм имеет линейную сложность.

Многие известные алгоритмы имеют квадратичную сложность O(n²). Это значит, что сложность алгоритма ограничена функцией с • n²:

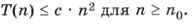
При этом если размер данных увеличивается в 10 раз, то количество операций (и время выполнения) увеличивается примерно в 100 раз. Пример такого алгоритма — сортировка методом прямого выбора, для которой число сравнений

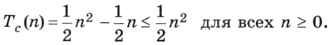
Алгоритм имеет асимптотическую сложность O(f(n)), если найдётся такая постоянная с, что для всех n ≥ n₀ выполняется условие Т(n) ≤ с • f(n).

Это значит, что при n ≥ n₀ график функции с • f(n) идёт выше, чем график функции Т(n) (рис. 5.9).

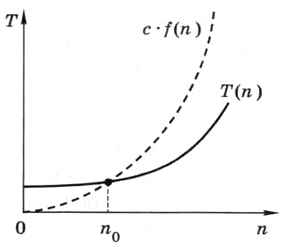
Рис. 5.9

Если количество операций не зависит от размера данных, то говорят, что сложность алгоритма O(1), т. е. количество операций меньше некоторой постоянной при любых n.

Существует также немало алгоритмов с кубической сложностью — O(n³). При больших значениях n алгоритм с кубической сложностью требует большего количества вычислений, чем алгоритм со сложностью O(n²), а тот, в свою очередь, работает дольше, чем алгоритм с линейной сложностью. Заметьте, что при малых значениях n всё может быть наоборот; это зависит от постоянной с для каждого из алгоритмов.

Известны и алгоритмы, для которых количество операций растёт быстрее, чем любой полином, например как O(2ⁿ) или O(n!). Они встречаются чаще всего в задачах оптимизации, которые решаются только методом полного перебора. Самая известная задача такого типа — это задача коммивояжёра (бродячего торговца), который должен посетить по одному разу каждый из указанных городов и вернуться в начальную точку. Для него нужно выбрать оптимальный маршрут, при котором стоимость поездки (или общая длина пути) будет минимальной.

Ещё один пример сложной задачи, которая решается только полным перебором всех вариантов, — задача выполнимости. Дано логическое выражение, которое содержит только имена логических переменных, скобки, а также операции «И», «ИЛИ» и «НЕ». Требуется определить, существует ли набор значений логических переменных, при котором заданное выражение истинно.

Следующая страница Алгоритмы поиска

Cкачать материалы урока