Уроки 77 - 79
Деревья. Основные понятия
(§43. Деревья)
Содержание урока
Обход двоичного дерева
Вычисление арифметических выражений
Использование связанных структур
Хранение двоичного дерева в массиве
Обход двоичного дерева
Обойти дерево — это значит «посетить» все узлы по одному разу. Если перечислить узлы в порядке их посещения, мы представим данные в виде списка.
Существуют несколько способов обхода дерева:
• КЛП — «корень - левый - правый» (обход в прямом порядке):
посетить корень
обойти левое поддерево
обойти правое поддерево
• ЛКП — «левый - корень - правый» (симметричный обход):
обойти левое поддерево
посетить корень
обойти правое поддерево
• ЛПК — «левый - правый - корень» (обход в обратном порядке):
обойти левое поддерево
обойти правое поддерево
посетить корень
Как видим, это рекурсивные алгоритмы. Они должны заканчиваться без повторного вызова, когда текущий корень — пустое дерево.
Рассмотрим дерево, которое может быть составлено для вычисления арифметического выражения (1 + 4) * (9 - 5) (рис. 6.13).
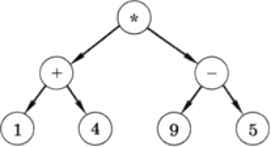
Рис. 6.13
Выражение вычисляется по такому дереву снизу вверх, т. е. посещение корня дерева — это последняя выполняемая операция.
Различные типы обхода дают последовательность узлов:
КЛП: * + 1 4 - 9 5
ЛКП: 1 + 4 * 9 - 5
ЛПК: 1 4 + 9 5 - *
В первом случае мы получили префиксную форму записи арифметического выражения, во втором — привычную нам инфиксную форму (только без скобок), а в третьем - постфиксную форму.
Напомним, что в префиксной и в постфиксной формах скобки не нужны.
Обход КЛП называется «обходом в глубину», потому что сначала мы идём вглубь дерева по левым поддеревьям, пока не дойдём до листа. Такой обход можно выполнить с помощью стека следующим образом:
записать в стек корень дерева нд пока стек не пуст выбрать узел V с вершины стека посетить узел V если у узла V есть правый сын то добавить в стек правого сына V все если у узла V есть левый сын то добавить в стек левого сына V все кц
На рисунке 6.14 показано изменение состояния стека при таком обходе дерева, изображенного на рис. 6.13. Под стеком записана метка узла, который посещается (например, данные из этого узла выводятся на экран).
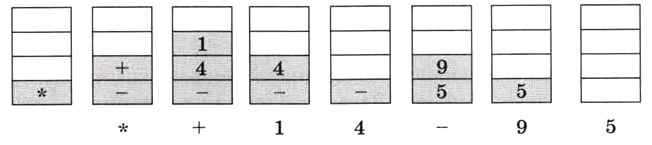
Рис. 6.14
Существует ещё один способ обхода, который называют обходом в ширину. Сначала посещают корень дерева, затем — всех его сыновей, затем — сыновей сыновей («внуков») и т. д., постепенно спускаясь на один уровень вниз. Обход в ширину для приведённого выше дерева даст такую последовательность посещения узлов:
* + - 1 4 9 5
Для того чтобы выполнить такой обход, применяют очередь. В очередь записывают узлы, которые необходимо посетить. На псевдокоде обход в ширину можно записать так:
записать в очередь корень дерева нц пока очередь не пуста выбрать первый узел V из очереди посетить узел V если у узла V есть левый сын то добавить в очередь левого сына V все если у узла V есть правый сын то добавить в очередь правого сына V все кц
Следующая страница  Вычисление арифметических выражений
Вычисление арифметических выражений

