Уроки 77 - 79
Деревья. Основные понятия
(§43. Деревья)

Содержание урока

Что такое дерево?

Деревья поиска

Обход двоичного дерева

Вычисление арифметических выражений

Использование связанных структур

Хранение двоичного дерева в массиве

Вопросы и задания

Задачи

Вычисление арифметических выражений

Один из способов вычисления арифметических выражений основан на использовании дерева. Сначала выражение, записанное в линейном виде (в одну строку), нужно «разобрать» и построить соответствующее ему дерево. Затем в результате прохода по этому дереву от листьев к корню вычисляется результат.

Для простоты будем рассматривать только арифметические выражения, содержащие числа и знаки четырёх арифметических операций: + - * /. Построим дерево для выражения

4 0 - 2 * 3 - 4 * 5

Нужно сначала найти последнюю операцию, просматривая выражение слева направо. Здесь последняя операция — это второе вычитание, оно оказывается в корне дерева (рис. 6.15).

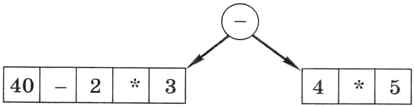
Рис. 6.15

Как выполнить этот поиск в программе? Известно, что операции выполняются в порядке приоритета (старшинства): сначала операции с более высоким приоритетом (слева направо), потом — с более низким (также слева направо). Отсюда следует важный вывод.

В корень дерева нужно поместить последнюю из операций с наименьшим приоритетом.

Теперь нужно построить таким же способом левое и правое поддеревья (рис. 6.16).

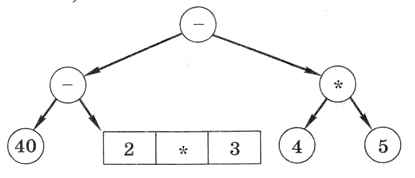
Рис. 6.16

Левое поддерево требует ещё одного шага (рис. 6.17).

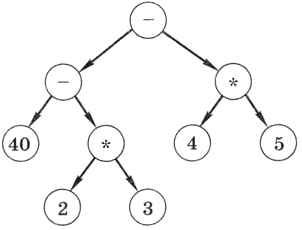
Рис. 6.17

Эта процедура рекурсивная, её можно записать в виде псевдокода:

найти последнюю выполняемую операцию 
если операций нет то 
создать узел-лист выход 
все
поместить найденную операцию в корень дерева 
построить левое поддерево 
построить правое поддерево

Рекурсия заканчивается, когда в оставшейся части строки нет ни одной операции, значит, там находится число (это лист дерева).

Теперь вычислим выражение по дереву. Если в корне находится знак операции, её нужно применить к результатам вычисления поддеревьев:

n1:=значение левого поддерева 
n2:=значение правого поддерева 
результат:=операция(n1,n2)

Снова получился рекурсивный алгоритм.

Возможен особый случай (на нём заканчивается рекурсия), когда корень дерева содержит число (т. е. это лист). Это число и будет результатом вычисления выражения.

Следующая страница Использование связанных структур

Cкачать материалы урока