Уроки 77 - 79
Деревья. Основные понятия
(§43. Деревья)
Содержание урока
Вычисление арифметических выражений
Использование связанных структур
Хранение двоичного дерева в массиве
Использование связанных структур
Поскольку двоичное дерево — это нелинейная структура данных, использовать динамический массив для размещения элементов не очень удобно (хотя возможно). Вместо этого будем использовать связанные узлы. Каждый такой узел — это структура, содержащая три области: область данных, ссылка на левое поддерево (указатель) и ссылка на правое поддерево (второй указатель). У листьев нет сыновей, в этом случае в указатели будем записывать значение nil (нулевой указатель). Дерево, состоящее из трёх таких узлов, показано на рис. 6.18.
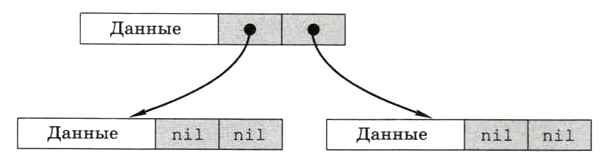
Рис. 6.18
В данном случае область данных узла будет содержать одно поле — символьную строку, в которую записывается знак операции или число в символьном виде.
Введём два новых типа: TNode — узел дерева, и PNode — указатель (ссылку) на такой узел:
type PNode = ˆTNode; TNode = record data: string[20]; left, right: PNode end;
Самый важный момент — выделение памяти под новую структуру. Предположим, что р — это переменная-указатель типа PNode. Для того чтобы выделить память под новую структуру и
записать адрес выделенного блока в р, используется процедура New (англ. new — новый):
New(р);
Как программа определяет, сколько памяти нужно выделить? Чтобы ответить на этот вопрос, вспомним, что указатель р указывает на структуру типа TNode, размер которой и определяет размер выделяемого блока памяти.
Для освобождения памяти служит процедура Dispose (англ. dispose — ликвидировать):
Dispose(р);
В основной программе объявим одну переменную типа PNode — это будет ссылка на корень дерева:
var Т: PNode;
Вычисление выражения сводится к двум вызовам функций:
Т:=Tree (s);
writeln('Результат: ', Calc(T));
Здесь предполагается, что арифметическое выражение записано в символьной строке s, функция Tree строит в памяти дерево по этой строке, а функция Calc — вычисляет значение выражения по готовому дереву.
При построении дерева нужно выделять в памяти новый узел и искать последнюю выполняемую операцию — это будет делать функция LastOp. Она возвращает 0, если ни одной операции не обнаружено, в этом случае создаётся лист — узел без потомков. Если операция найдена, её обозначение записывается в поле data, а в указатели записываются адреса поддеревьев, которые строятся рекурсивно для левой и правой частей выражения:
function Tree(s: string): PNode;
var k: integer;
begin
New(Tree); {выделить память}
k:=LastOp(s);
if k=0 then begin {создать лист}
Тгееˆ.data:=s;
Тгееˆ.left:=nil;
Treeˆ.right:=nil;
end
else begin {создать узел-операцию}
Treeˆ.data:=s[k);
Treeˆ.left:=Tree(Copy(s,1,k—1));
Treeˆ.right:=Tree(Copy(s,k+1,Length(s)-k))
end
end;
Функция Calc тоже будет рекурсивной:
function Calc(Tree: PNode): integer; var n1, n2, res: integer; begin if Treeˆ.left = nil then Val(ТгееЛ.data, Calc, res) else begin n1:=Calc(Treeˆ.left); n2:=Calc(Тгееˆ.right); case Тгееˆ.data[1] of '+': Calc:=n1+n2; '-': Calc:=n1-n2; '*': Calc:=n1*n2; '/': Calc:=n1 div n2; else Calc:=MaxInt end end end;
Если ссылка, переданная функции, указывает на лист (нет левого поддерева), то значение выражения — это результат преобразования числа из символьной формы в числовую (с помощью процедуры Val). В противном случае вычисляются значения для левого и правого поддеревьев и к ним применяется операция, указанная в корне дерева. В случае ошибки (неизвестной операции) функция возвращает значение Maxlnt — максимальное целое число.
Осталось написать функцию LastOp. Нужно найти в символьной строке последнюю операцию с минимальным приоритетом. Для этого составим функцию, возвращающую приоритет операции (переданного ей символа):
function Priority(op: char): integer; begin case op of '+','-': Priority:=1; '*','/': Priority:=2; else Priority:=100 end end;
Сложение и вычитание имеют приоритет 1, умножение и деление — приоритет 2, а все остальные символы (не операции) — приоритет 100 (условное значение).
Функция La stop может выглядеть так:
function LastOp(s: string): integer; var i, minPrt: integer; begin minPrt:=50; LastOp:=0; for i:=l to Length (s) do if Priority(s[i])<=minPrt then begin minPrt:=Priority(s[i]); LastOp:=i end end;
Обратите внимание, что в условном операторе указано нестрогое неравенство, чтобы найти именно последнюю операцию с наименьшим приоритетом. Начальное значение переменной minPrt можно выбрать любое между наибольшим приоритетом операций (2) и условным кодом не-операции (100). Тогда если найдена любая операция, условный оператор срабатывает, а если в строке нет операций, условие всегда ложно и в переменной LastOp остается начальное значение 0.
Следующая страница  Хранение двоичного дерева в массиве
Хранение двоичного дерева в массиве

