Уроки 80 - 83
Графы. Основные понятия
(§44. Графы)
Содержание урока
Что такое граф?
Что такое граф?
Как вы знаете из курса 10 класса, граф — это набор узлов (вершин) и связей между ними (рёбер). Информацию об узлах и связях графа обычно хранят в виде таблицы специального вида — матрицы смежности (рис. 6.20).
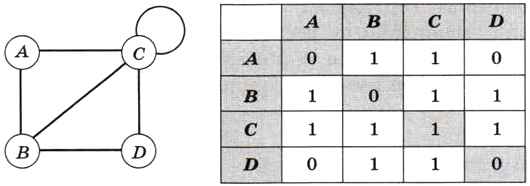
Рис. 6.20
Единица на пересечении строки А и столбца В означает, что между узлами А и В есть связь. Ноль указывает на то, что связи нет. Матрица смежности симметрична относительно главной диагонали (выделенные фоном ячейки в таблице). Единица на главной диагонали обозначает петлю — ребро, которое начинается и заканчивается в одной и той же вершине (в данном примере — в вершине С). Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости, но матрица смежности не даёт никакой информации о том, как именно следует располагать узлы друг относительно друга. Для таблицы, приведённой на рис. 6.20, возможны, например, такие варианты (рис. 6.21).
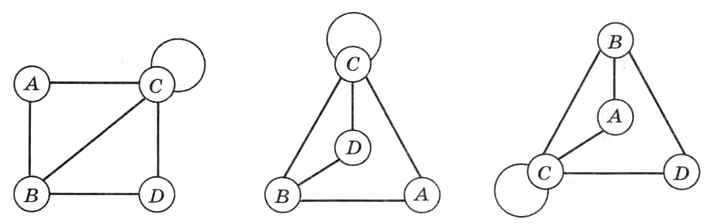
Рис. 6.21
В рассмотренном примере все узлы связаны, т. е. между любой парой узлов существует путь — последовательность рёбер, по которым можно перейти из одного узла в другой. Такой граф называется связным.
Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа, в котором нет замкнутых путей — циклов.
Если для каждого ребра указано направление, граф называют ориентированным (орграфом). Рёбра орграфа называют дугами. Его матрица смежности не всегда симметричная. Единица, стоящая на пересечении строки А и столбца В, говорит о том, что существует дуга из вершины А в вершину В (рис. 6.22).
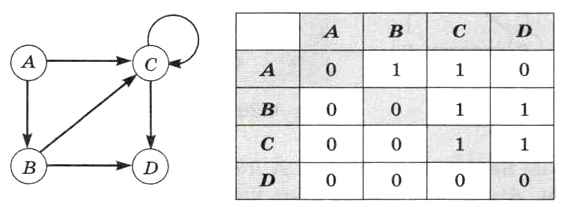
Рис. 6.22
Часто с каждым ребром связывают некоторое число — вес ребра. Это может быть, например, расстояние между городами или стоимость проезда. Такой граф называется взвешенным. Информация о взвешенном графе хранится в виде весовой матрицы, содержащей веса рёбер (рис. 6.23).
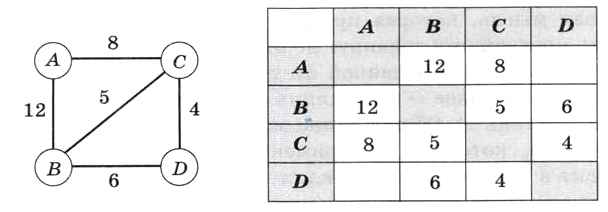
Рис. 6.23
У взвешенного орграфа весовая матрица может быть несимметрична относительно главной диагонали (рис. 6.24).
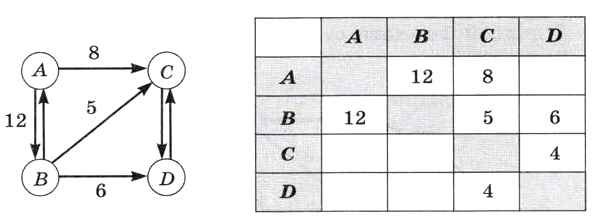
Рис. 6.24
Если связи между двумя узлами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в неё условный код, например 0, -1 или очень большое число (со), в зависимости от задачи.
Следующая страница  «Жадные» алгоритмы. Задача 1
«Жадные» алгоритмы. Задача 1

