Уроки 80 - 83
Графы. Основные понятия
(§44. Графы)
Содержание урока
«Жадные» алгоритмы. Задача 2
«Жадные» алгоритмы. Задача 2
Задача 2. В стране Лимонии есть N городов, которые нужно соединить линиями связи. Между какими городами нужно проложить линии связи, чтобы все города были связаны в одну систему и общая длина линий связи была наименьшей?
В теории графов эта задача называется задачей построения минимального остовного дерева (т. е. дерева, связывающего все вершины). Остовное дерево для связного графа с N вершинами имеет N - 1 ребро.
Рассмотрим «жадный» алгоритм решения этой задачи, предложенный Крускалом:
1) начальное дерево — пустое;
2) на каждом шаге к дереву добавляется ребро минимального веса, которое ещё не входит в дерево и не приводит к появлению цикла в дереве.
На рисунке 6.27 показано минимальное остовное дерево для одного из рассмотренных выше графов (сплошные жирные линии).
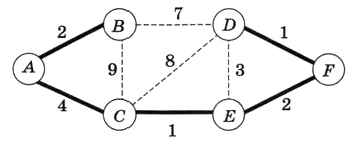
Рис. 6.27
Здесь возможна такая последовательность добавления рёбер: СЕ, DF, АВ, EF, АС. Обратите внимание, что после добавления ребра EF следующее «свободное» ребро минимального веса — это DE (длина 3), но оно образует цикл с рёбрами DF и EF, поэтому не было включено в дерево.
При программировании этого алгоритма сразу возникает вопрос: как определить, что ребро ещё не включено в дерево и не образует цикла в нём? Существует очень красивое решение этой проблемы, основанное на «раскраске» вершин.
Сначала все вершины «раскрашиваются» в разные цвета (т. е. им присваиваются разные числовые коды):
for i:=l to N do col[i]:=i;
Здесь N — количество вершин, a col — целочисленный массив с индексами от 1 до N.
Затем в цикле N — 1 раз (именно столько рёбер нужно включить в дерево) выполняем следующие операции:
1) ищем ребро минимальной длины среди всех рёбер, концы которых окрашены в разные цвета;
2) найденное ребро (iMin,jMin) добавляется в список выбранных, и все вершины, имеющие цвет col[jMin], перекрашиваются в цвет col[iMin].
Приведём полностью основной цикл программы:
for k:=1 to N-1 do begin
{поиск ребра с минимальным весом}
min:=MaxInt;
for i:=1 to N do
for j:=1 to N do
if (col[i]<>col[j]) and (W[i,j] < min)
then begin
iMin:=i; jMin:=j; min:=W[i,j];
end;
{добавление ребра в список выбранных}
ostov[k,1]:=iMin;
ostov[k,2}:=jMin;
{перекрашивание вершин}
for i:=1 to N do
if col[i]=col[jMin] then
col[i]:=col[iMin];
end;
Здесь W — целочисленная матрица размера N x N (индексы строк и столбцов начинаются с 1); ostov — целочисленный массив из N-1 строк и двух столбцов для хранения выбранных рёбер (для каждого ребра хранятся номера двух вершин, которые оно соединяет).
После окончания цикла остаётся вывести результат — рёбра из массива ostov:
for i:=1 to N-1 do
writeln('(', ostov[i,1], ostov[i,2], ')');
Следующая страница 
Кратчайшие маршруты
Cкачать материалы урока
