Уроки 80 - 83
Графы. Основные понятия
(§44. Графы)

Содержание урока

Что такое граф?

«Жадные» алгоритмы. Задача 1

«Жадные» алгоритмы. Задача 2

Кратчайшие маршруты

Некоторые задачи

Вопросы и задания

Задачи

Кратчайшие маршруты

В предыдущем пункте мы познакомились с задачей выбора кратчайшего маршрута и увидели, что в ней «жадный» алгоритм не всегда даёт правильное решение. В 1960 г. Э. Дейкстра предложил алгоритм, позволяющий найти все кратчайшие расстояния от одной вершины графа до всех остальных и соответствующие им маршруты. Предполагается, что длины всех рёбер (расстояния между вершинами) положительные.

Рассмотрим уже знакомую схему, в которой не сработал «жадный» алгоритм (рис. 6.28).

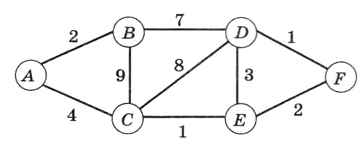
Рис. 6.28

Алгоритм Дейкстры использует дополнительные массивы: в одном (назовём его i?) хранятся кратчайшие (на данный момент) расстояния от исходной вершины до каждой из вершин графа, а во втором (массив Р) — вершина, из которой нужно «приехать» в данную вершину.

Сначала записываем в массив R расстояния от исходной вершины А до всех вершин, а в соответствующие элементы массива Р — вершину А (рис. 6.29).

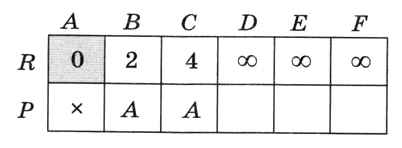
Рис. 6.29

Знак оо обозначает, что прямого пути из вершины А в данную вершину нет (в программе вместо оо можно использовать очень большое число). Таким образом, вершина А уже рассмотрена и соответствующий элемент массива R выделен фоном. В первый элемент массива Р записан символ х, обозначающий начальную точку маршрута (в программе можно использовать несуществующий номер вершины, например 0).

Из оставшихся вершин находим вершину с минимальным значением в массиве R: это вершина В. Теперь проверяем пути, проходящие через эту вершину: не позволят ли они сократить маршрут к другим вершинам, которые мы ещё не посещали. Идея состоит в следующем: если сумма весов W[x,z] + W[z,y] меньше, чем вес W[x,y], то из вершины X лучше ехать в вершину Y не напрямую, а через вершину Z (рис. 6.30).

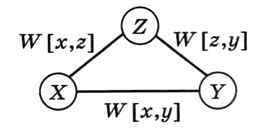
Рис. 6.30

Проверяем наш граф: ехать из А в С через В невыгодно (получается путь длиной 11 вместо 4), а вот в вершину D можно проехать (путь длиной 9), поэтому запоминаем это значение вместо со в массиве R и записываем вершину В на соответствующее место в массив Р («в D приезжаем из В») (рис. 6.31).

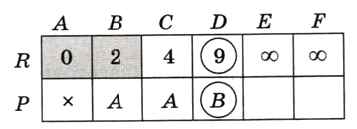
Рис. 6.31

Вершины Е и F по-прежнему недоступны.

Следующей рассматриваем вершину С (для неё значение в массиве R минимально). Оказывается, что через неё можно добраться до Е (длина пути 5) (рис. 6.32).

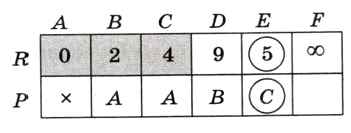
Рис. 6.32

Затем посещаем вершину Е, которая позволяет достигнуть вершины F и улучшить минимальную длину пути до вершины D (рис. 6.33).

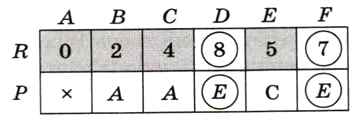
Рис. 6.33

После рассмотрения вершин F и D таблица не меняется. Итак, мы получили, что кратчайший маршрут из А в F имеет длину 7, причём он приходит в вершину F из Е. Как же получить весь маршрут? Нужно просто посмотреть в массиве Р, откуда лучше всего ехать в Е — выясняется, что из вершины С, а в вершину С — напрямую из начальной точки А (рис. 6.34).

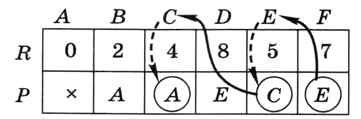
Рис. 6.34

Поэтому кратчайший маршрут A-C-E-F. Обратите внимание, что этот маршрут «раскручивается» в обратную сторону, от конечной вершины к начальной. Заметим, что полученная таблица содержит все кратчайшие маршруты из вершины А во все остальные вершины, а не только из А в F.

Алгоритм Дейкстры можно рассматривать как своеобразный «жадный» алгоритм: действительно, на каждом шаге из всех не- выбранных вершин выбирается такая вершина X, что длина пути от А до X минимальна, если ехать только через уже выбранные вершины. Однако можно доказать, что это расстояние — действительно минимальная длина пути от А до X. Предположим, что для всех предыдущих выбранных вершин это свойство справедливо. При этом X — это ближайшая невыбранная вершина, которую можно достичь из начальной точки, проезжая только через выбранные вершины. Все остальные пути в X, проходящие через ещё не выбранные вершины, будут длиннее, поскольку все рёбра имеют положительную длину. Таким образом, найденная длина пути из А в X — минимальная.

После завершения алгоритма, когда все вершины выбраны, в массиве R находятся длины кратчайших маршрутов.

В программе объявим константу и переменные:

const N = 6;
var W: array[1..N,1..N] of integer;
	active: array [1..N] of boolean;
	R, P: array [1..N] of integer;
	i, j, min, kMin: integer;

Массив W — это весовая матрица, её удобно вводить из файла. Логический массив active хранит состояние вершин (просмотрена или не просмотрена): если значение active[i] истинно, то вершина активна (ещё не просматривалась).

В начале программы присваиваем начальные значения (объяснение см. выше), сразу помечаем, что вершина 1 просмотрена (не активна), с неё начинается маршрут.

for i:=l to N do begin
	active[i]:=True;
	R[i]:= W[l,i];
	P[i]:=1;
end;
active[1]:=False;
P[1]:=0;

В основном цикле, который выполняется N - 1 раз (так, чтобы все вершины были просмотрены), среди активных вершин ищем вершину с минимальным соответствующим значением в массиве R и проверяем, не лучше ли ехать через неё:

for i:=1 to N-1 do begin
		{поиск новой рабочей вершины R[j] -> min} 
	min:=MaxInt; {максимальное целое число) 
	for j:=l to N do
		if active[j] and (R[j]<min) then begin 
			min:=R[j]; kMin:=j; 
		end;
	active[kMin]:=False;
		{проверка маршрутов через вершину kMin) 
	for j:=l to N do
		if R[kMin]+W[kMin,j]<R[j] then begin 
			R[j]:=R[kMin]+W[kMin,j];
			P[j]:=kMin 
		end
end;

В конце программы выводим оптимальный маршрут в обратном порядке:

i:=N;
while i<>0 do begin {для начальной вершины P[i]=0) write (i : 5);
i:=P[i] {переход к следующей вершине] 
end;

Алгоритм Дейкстры, как мы видели, находит кратчайшие пути из одной заданной вершины во все остальные. Найти все кратчайшие пути (из любой вершины в любую другую) можно с помощью алгоритма Флойда—Уоршелла, основанного на той же самой идее сокращения маршрута (иногда бывает короче ехать через промежуточные вершины, чем напрямую):

for k:=1 to N do 
	for i:=1 to N do 
		for j:=1 to N do
			if w [i, k]+W [k, j ] < W[i,j] then 
				W[i,j]:= W[i,k] + W [k, j ] ;

В результате исходная весовая матрица графа W размером N х N превращается в матрицу, хранящую длины оптимальных маршрутов. Для того чтобы найти сами маршруты, нужно использовать еще одну дополнительную матрицу, которая выполняет ту же роль, что и массив Р в алгоритме Дейкстры.

Следующая страница Некоторые задачи

Cкачать материалы урока