Уроки 10 - 12
Модели ограниченного и неограниченного роста
(§10. Математические модели в биологии)

Содержание урока

Модель неограниченного роста

Модель ограниченного роста

Взаимодействие видов

Обратная связь. Саморегуляция

Вопросы и задания

Задачи

Взаимодействие видов

Все модели, которые мы рассматривали выше, описывали изменение одного вида. На самом деле на одной территории всегда живут несколько видов животных, которые соперничают друг с другом. В простейшем случае это соперничество за еду (например, между белками и бурундуками). Однако наиболее интересна модель «хищник — жертва», в которой один вид — хищники (например, щуки), а второй — их пища (караси).

Сначала построим модели двух видов по отдельности. Изменение численности карасей N_i описывается уже известной нам моделью ограниченного роста:

N_i+1 = (1 + K_L) • N_i, K_L = K • (L - N_i / L).

Будем считать, что щуки могут питаться только карасями ¹. Тогда без карасей они просто погибают, и модель изменения их численности имеет вид:

Z_i+1 = (1 - D) - Z_i,

где D — коэффициент смертности щук (для простоты будем считать его постоянным).

---

¹ Конечно, в самом деле, это предположение чаще всего неверно, но мы используем его для простоты модели.

---

Объединив две модели, мы не получаем систему, потому что никак не учитывается связь между численностью карасей и щук, живущих в одном водоёме. В результате численность карасей со временем станет равна L, а щуки вымрут, хотя вокруг полно еды.

Чтобы построить системную модель, предположим, что частота встреч карасей и щук пропорциональна произведению их численностей: N_i • Z_i. В результате этих встреч каждый год гибнет b_N-N_i-Z_i карасей, но появляется b_z-N_i-Z_i новых щук. Здесь b_N и bz — это некоторые коэффициенты, которые определяются экспериментально. Таким образом, полная модель-система состоит из двух связанных уравнений:

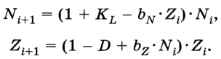
На рисунке 2.16 показаны графики изменения численности карасей и щук, полученные при L = 100, N₀ = 50, Z₀ — 10, d = 0,8, b_N = 0,01 и b_z = 0,012. Сначала мы видим «переходный период», когда численность карасей и щук довольно сильно меняется, а затем наступает равновесие — количество рыб обоих видов остаётся примерно постоянным. Обратите внимание, что численность карасей не достигает предельного значения L — щуки мешают. Вместе с тем количество щук не растёт бесконтрольно — не хватает еды. Таким образом, в природных системах соблюдается равновесие.

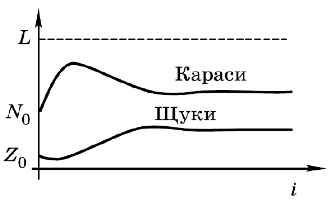
Рис. 2.16

Следующая страница Обратная связь. Саморегуляция

Cкачать материалы урока