Уроки 10 - 12
Модели ограниченного и неограниченного роста
(§10. Математические модели в биологии)

Содержание урока

Модель неограниченного роста

Модель ограниченного роста

Взаимодействие видов

Обратная связь. Саморегуляция

Вопросы и задания

Задачи

Обратная связь. Саморегуляция

Модели неограниченного и ограниченного роста популяции животных, которые изучались в предыдущем пункте, можно изобразить в виде схем следующим образом (рис. 2.17).

В первом случае (модель неограниченного роста) коэффициент прироста К жёстко задан и не меняется. Такая модель адекватна только при малых интервалах наблюдения.

В модели ограниченного роста коэффициент прироста K_L не фиксирован, а меняется в зависимости от ситуации. На него влияют две величины — максимальная численность популяции L и текущая численность N. Переходя на язык теории управления (см. § 4), величину L можно рассматривать как «цель», заданную природой, она определяется природными условиями (количеством корма, погодой и т. п.).

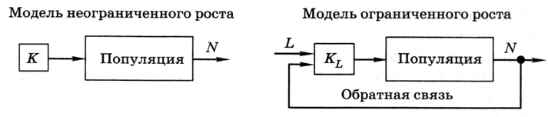
Рис. 2.17

Зависимость коэффициента K_L от численности N — это обратная связь, с помощью которой регулируется численность. Если N < L, т. е. фактическая численность меньше «заданной», начинается прирост численности (K_L > 0). Ситуация, когда N > L, — это перенаселение, при котором K_L < 0 и животные начинают вымирать. Как мы видели, при N = L получается нулевой прирост, численность не меняется.

Если в какой-то момент популяция резко сокращается (например, рыбы отравились химическими веществами, сброшенными в воду), после устранения проблемы численность снова восстанавливается и достигает максимального уровня L (рис. 2.18). Так работает саморегуляция.

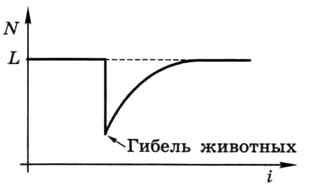
Рис. 2.18

Саморегуляция — это способность системы поддерживать своё внутреннее состояние за счёт связей между элементами.

Саморегуляция — очень важное свойство живых организмов, которое позволяет им выживать при изменениях внешних условий. Например, теплокровные животные поддерживают постоянную температуру тела, бактерии и водоросли поддерживают постоянную солёность и состав морской воды.

Строго говоря, если рассмотреть блок «популяция» на схеме как подсистему, мы тоже найдём в ней внутреннюю обратную связь, поскольку численность на очередном шаге N_i+1 зависит от численности на предыдущем шаге N_i. На схеме (рис. 2.19) квадратик с крестиком обозначает умножение, а блок с буквой τ — запаздывание (задержку), которое позволяет в течение одного шага помнить последнее значение N_i.

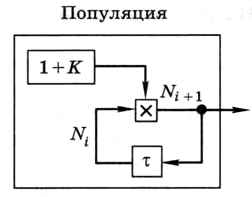
Рис. 2.19

Несмотря на обратную связь, возможности саморегуляции в такой системе очень ограничены: при К > 0 численность будет бесконечно расти (нет саморегуляции), а при К < 0 популяция вымирает (равновесие наступает только при N = 0).

Пример саморегуляции в системе «хищник — жертва» мы рассматривали в предыдущем пункте. В этой системе три канала обратной связи (не считая внутренних, в каждой популяции) (рис. 2.20).

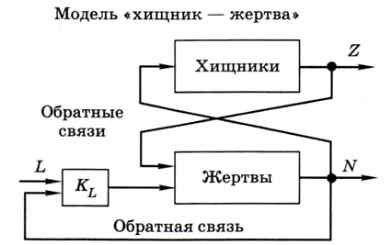
Рис. 2.20

Саморегуляция «работает» только при небольших отклонениях от состояния равновесия. Если серьезно нарушить баланс, система не сможет восстановиться. В последние столетия человек все активнее вмешивается в жизнь природы, в результате сокращаются леса и зоны с плодородной почвой, изменяется климат, вымирают все новые и новые виды животных. Нарушение саморегуляции в масштабе Земли может поставить под угрозу жизнь всего человечества.

Следующая страница Вопросы и задания

Cкачать материалы урока