Уроки 10 - 12
Модели ограниченного и неограниченного роста
(§10. Математические модели в биологии)

Содержание урока

Модель неограниченного роста

Модель ограниченного роста

Взаимодействие видов

Обратная связь. Саморегуляция

Вопросы и задания

Задачи

Задачи

1. Постройте графики изменения численности популяции для моделей ограниченного и неограниченного роста при А = 100, К = 0,5 и L = 1000. Определите, через сколько интервалов наблюдения модель неограниченного роста перестаёт быть адекватной (отклонение от модели ограниченного роста составляет более 10%).

2. Для предыдущей задачи выполните моделирование с учётом отлова (R = 40):

• определите количество животных в состоянии равновесия теоретически и по результатам моделирования; зависит ли оно от начальной численности?
• определите, на что влияет начальная численность животных;
• найдите максимальный отлов R, при котором популяция не вымирает.

*3. При эпидемии гриппа число больных N изменяется по формуле

N_i+1 = N_i + Z_i+1 - V_i+1,

где Z_i — количество заболевших в i-й день, a V_i — количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:

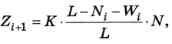
где L — общая численность жителей, К — коэффициент роста и W_i — число переболевших (тех, кто уже переболел и выздоровел и поэтому больше не заболеет):

W_i+1 = W_i + V_i+1.

Считается, что все заболевшие выздоравливают через 7 дней и больше не болеют. Выполните моделирование при L = 1000 и К = 0,5, считая, что в начале эпидемии заболел 1 человек. Ответьте на следующие вопросы:

• Когда закончится эпидемия?
• Сколько человек переболеет, а сколько вообще не заболеет гриппом?
• Каково максимальное число больных в один день?

4. Выполните моделирование системы «хищник — жертва» при параметрах, указанных в тексте параграфа. Ответьте на следующие вопросы:

• Сколько карасей и щук живут в водоёме в состоянии равновесия?
• Что влияет на количество рыб в состоянии равновесия: начальная численность или значения коэффициентов модели?
• На что влияет начальная численность?
• При каких значениях коэффициентов модель становится неадекватна? В чём это выражается?
• При каких значениях коэффициентов щуки вымирают, а численность карасей достигает предельно возможного значения? Как вы можете объяснить это с точки зрения биологии?

5. Белки и бурундуки живут в одном лесу и едят примерно одно и то же (конкурируют за пищу). Модель, описывающая изменение численности двух популяций, имеет вид:

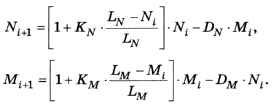
Здесь N и М — численность белок и бурундуков; L_N и L_M — их максимальные численности; K_N и К_M — коэффициенты прироста; D_N и D_M — коэффициенты взаимного влияния. Выполните моделирование при N₀ = 10, М₀ = 20, L_N = 70, L_M = 50, К_N = К_M = 0,7 и D_N = D_M = 0,1. Постройте графики изменения численности обоих видов. Ответьте на следующие вопросы:

• Является ли эта модель системной?
• Какова численность белок и бурундуков в состоянии равновесия?
• Что влияет на состояние равновесия?
• На что влияет начальная численность животных?
• При каком значении коэффициента Dm бурундуки вымрут через 25 лет?
• При каких значениях коэффициентов модель становится неадекватной?
• Какую аналогичную модель взаимного влияния трёх видов вы можете предложить?

Следующая страница §10. Математические модели в биологии

Cкачать материалы урока