Уроки 21 - 32
Моделирование корреляционных зависимостей (§19)
Практическая работа № 3.4. "Расчет корреляционных зависимостей"
Содержание урока
Компьютерное информационное моделирование (§16)
Моделирование зависимостей между величинами (§17)
Модели статистического прогнозирования (§18)
Моделирование корреляционных зависимостей (§19)
Построение регрессионных математических моделей
Практическая работа № 3.4 Расчет корреляционных зависимостей
Модели оптимального планирования (§20)
Итоговое тестирование по теме "Информационное моделирование"
Моделирование корреляционных зависимостей (§19)
Построение регрессионных математических моделей
Регрессионные математические модели строятся в тех случаях, когда известно, что зависимость между двумя факторами существует и требуется получить ее математическое описание. А сейчас мы рассмотрим задачи другого рода. Пусть важной характеристикой некоторой сложной системы является фактор А. На него могут оказывать влияние одновременно многие другие факторы: В, С, D и т. д. Мы рассмотрим два типа задач.
1) Оказывает ли фактор В какое-либо заметное регулярное влияние на фактор А?
2) Какие из факторов В, С, D и т. д. оказывают наибольшее влияние на фактор А?
В качестве примера сложной системы будем рассматривать школу. Пусть для первого типа задач фактором А является средняя успеваемость учащихся школы, фактором В — финансовые расходы школы на хозяйственные нужды: ремонт здания, обновление мебели, эстетическое оформление помещения и т. п. Здесь влияние фактора В на фактор А не очевидно. Наверное, гораздо сильнее на успеваемость влияют другие причины: уровень квалификации учителей, контингент учащихся, уровень технических средств обучения и др.
Специалисты по статистике знают, что для того, чтобы выявить зависимость от какого-то определенного фактора, нужно максимально исключить влияние других факторов. Проще говоря, собирая информацию из разных школ, нужно выбирать такие школы, в которых приблизительно одинаковый контингент учеников, квалификация учителей и пр., но хозяйственные расходы разные (у одних школ могут быть богатые спонсоры, у других — нет).
Итак, пусть хозяйственные расходы школы выражаются количеством рублей, отнесенных к числу учеников в школе (руб./чел.), потраченных за определенный период времени (например, за последние 5 лет). Успеваемость же пусть оценивается средним баллом учеников школы по результатам окончания последнего учебного года. Еще раз обращаем ваше внимание на то, что в статистических расчетах обычно используются относительные и усредненные величины.
Итоги сбора данных по 20 школам, введенные в электронную таблицу, представлены на рис. 3.7. На рис. 3.8 приведена точечная диаграмма, построенная по этим данным.
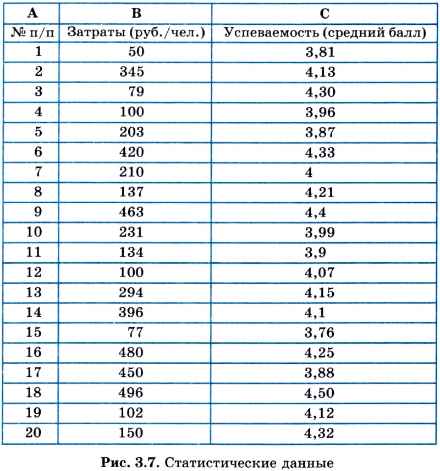
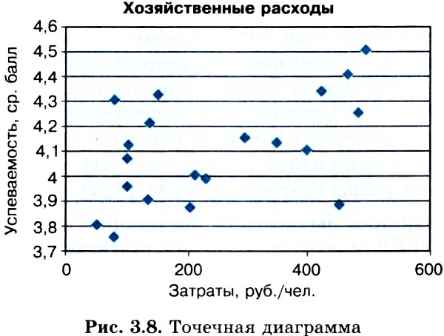
Значения обеих величин: финансовых затрат и успеваемости учеников — имеют значительный разброс и, на первый взгляд, взаимосвязи между ними не видно. Однако она вполне может существовать.
Следующая страница  Корреляционные зависимости
Корреляционные зависимости

