Уроки 21 - 32
Моделирование корреляционных зависимостей (§19)
Практическая работа № 3.4. "Расчет корреляционных зависимостей"
Содержание урока
Компьютерное информационное моделирование (§16)
Моделирование зависимостей между величинами (§17)
Модели статистического прогнозирования (§18)
Моделирование корреляционных зависимостей (§19)
Построение регрессионных математических моделей
Корреляционные зависимости
Практическая работа № 3.4 Расчет корреляционных зависимостей
Модели оптимального планирования (§20)
Итоговое тестирование по теме "Информационное моделирование"
Моделирование корреляционных зависимостей (§19)
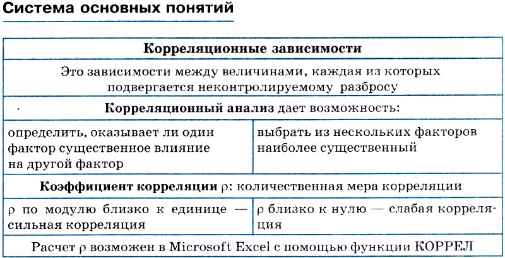
Корреляционные зависимости
 Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционными зависимостями.
Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционными зависимостями.
Раздел математической статистики, который исследует такие зависимости, называется корреляционным анализом. Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру такой зависимости.
Оценку корреляции величин начинают с высказывания гипотезы о возможном характере зависимости между их значениями. Чаще всего допускают наличие линейной зависимости. В таком случае мерой корреляционной зависимости является величина, которая называется коэффициентом корреляции. Как и прежде, мы не будем писать формулы, по которым этот коэффициент вычисляется; их написать нетрудно, гораздо труднее понять, почему они именно такие. На данном этапе достаточно знать следующее:
• коэффициент корреляции (обычно обозначаемый греческой буквой ρ) есть число из диапазона от -1 до +1;
• если это число по модулю близко к 1, то имеет место сильная корреляция; если к 0, то слабая;
• близость ρ к +1 означает, что возрастанию значений одного набора соответствует возрастание значений другого набора, близость ρ к -1 означает, что возрастанию значений одного набора соответствует убывание значений другого набора;
• значение ρ легко найти с помощью Excel, так как в эту программу встроены соответствующие формулы.
В Excel функция вычисления коэффициента корреляции называется KOPPEЛ и входит в группу статистических функций. Покажем, как ею воспользоваться. На том же листе Excel, где находится таблица, представленная на рис. 3.7, надо установить курсор на любую свободную ячейку и запустить функцию KOPPEЛ. Она запросит два диапазона значений. Укажем, соответственно, В2:В21 и С2:С21. После их ввода будет выведен ответ: ρ = 0,500273843. Эта величина говорит о среднем уровне корреляции.
Наличие зависимости между хозяйственными затратами школы и успеваемостью нетрудно понять. Ученики с удовольствием ходят в чистую, красивую, уютную школу, чувствуют там себя, как дома, и поэтому лучше учатся.
В следующем примере проводится исследование по определению зависимости успеваемости учащихся старших классов от двух факторов: обеспеченности школьной библиотеки учебниками и оснащения школы компьютерами. И та, и другая характеристика количественно выражается в процентах от нормы. Нормой обеспеченности учебниками является их полный комплект, т. е. такое количество, когда каждому ученику выдаются из библиотеки все нужные ему для учебы книги. Нормой оснащения компьютерами будем считать такое их количество, при котором на каждых четырех старшеклассников в школе приходится один компьютер. Предполагается, что компьютерами ученики пользуются не только на информатике, но и на других уроках, а также во внеурочное время.
В таблице, изображенной на рис. 3.9, приведены результаты измерения обоих факторов в 11 разных школах. Напомним, что влияние каждого фактора исследуется независимо от других (т. е. влияние других существенных факторов должно быть приблизительно одинаковым).
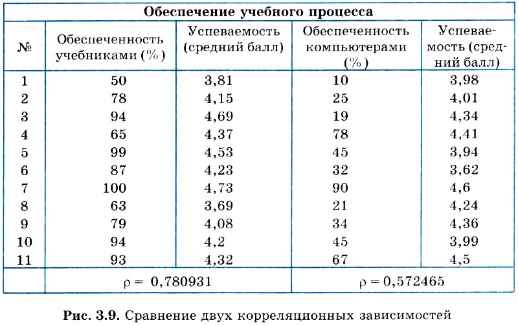
Для обеих зависимостей получены коэффициенты линейной корреляции. Как видно из таблицы, корреляция между обеспеченностью учебниками и успеваемостью сильнее, чем корреляция между компьютерным обеспечением и успеваемостью (хотя и тот, и другой коэффициенты корреляции не очень большие). Отсюда можно сделать вывод, что пока еще книга остается более значительным источником знаний, чем компьютер.
Следующая страница  Вопросы и задания
Вопросы и задания

