Уроки 13 - 14
Моделирование движения. Дискретизация
(§2. Моделирование движения)

Содержание урока

Движение с сопротивлением

Дискретизация

Компьютерная модель

Вопросы и задания

Задачи

Движение с сопротивлением

На уроках физики вы изучали в основном две модели движения: равномерное (когда равнодействующая всех сил равна нулю) и равноускоренное (когда равнодействующая постоянна). Например, движение тела, брошенного под углом к горизонту, обычно раскладывается на равномерное движение по горизонтали и равноускоренное движение по вертикали (под действием силы тяжести).

В реальных ситуациях силы, действующие на систему, постоянно изменяются, поэтому ускорение тоже будет переменным, и упомянутые простейшие модели использовать нельзя — они неадекватны. Для примера мы разберём задачу, в которой важную роль играют силы сопротивления среды.

Рассмотрим движение мяча, который представляет собой шар радиуса r и массы m, брошенного вертикально вверх со скоростью v₀. Нужно найти, на какую высоту поднимется мяч, и скорость, с которой он упадёт на землю.

На мяч в полёте действуют две силы (рис. 2.13):

• сила тяжести G (она направлена вертикально вниз);
• сила сопротивления F, которая направлена противоположно вектору текущей скорости v.

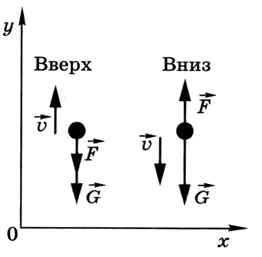
Рис. 2.13

Будем работать с проекциями всех сил на вертикальную ось, за положительное направление примем направление вверх. Тогда проекция силы тяжести G = -mg, где g — ускорение свободного падения.

Сила сопротивления зависит от формы и размеров тела, его скорости и свойств среды. На малых скоростях сила сопротивления пропорциональна скорости, а при увеличении скорости пропорциональна её квадрату:

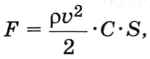
где ρ — плотность среды (для воздуха ρ ≈ 1,23 кг/м3), v — скорость тела, S — площадь поперечного сечения (для шара S = π • r²), а коэффициент сопротивления С зависит от формы тела и определяется экспериментально (для шара С ≈ 0,4).

Чтобы показать, что вектор силы сопротивления всегда направлен противоположно вектору скорости, часто используют такую запись:

Ускорение определяется по второму закону Ньютона:

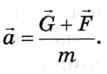
Сила сопротивления F зависит от скорости, которая меняется. Поэтому ускорение тоже будет переменным, и модель равноускоренного движения применить нельзя. Исследовать такое движение теоретически довольно сложно, поэтому мы используем имитационную модель.

Следующая страница Дискретизация

Cкачать материалы урока