Уроки 13 - 14
Моделирование движения. Дискретизация
(§2. Моделирование движения)

Содержание урока

Движение с сопротивлением

Дискретизация

Компьютерная модель

Вопросы и задания

Задачи

Дискретизация

В конце XX века задачи моделирования законов движения решались с помощью аналоговых вычислительных машин, которые работали с аналоговыми сигналами. Мы будем использовать цифровой (дискретный) компьютер, поэтому нужно выполнить дискретизацию — перейти к дискретной модели, которая описывает движение мяча в отдельные моменты времени с некоторым шагом :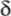

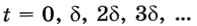
Нам нужно построить такую модель, которая позволит вычислить скорость и высоту мяча в момент t_i+1 = (i + 1) • 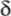при известных данных в момент t_i = i • . Чтобы использовать известные формулы для равноускоренного движения, мы предположим, что на отрезке [t_i, t_i+1] ускорение изменяется очень мало и можно считать его примерно постоянным. Конечно, фактически это не так, но при маленьком интервале 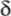ошибка будет небольшой.

Как выбрать 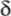? Понятно, что чем меньше 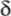, тем точнее модель и меньше ошибка моделирования. Вместе с тем при уменьшении 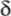возрастает объём расчётов, поэтому нужно попытаться найти «золотую середину». Можно, например, начать с большого 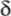(допустим, 1 с) и постепенно уменьшать его, повторяя моделирование до тех пор, пока результаты практически перестанут изменяться.

Итак, предположим, что в момент t_i скорость мяча¹ равна v_i и он находится на высоте y_i. Определим силу сопротивления и ускорение в этот момент:

---

¹ Здесь и далее мы фактически рассматриваем проекции скорости, ускорения и сил на вертикальную ось.

---

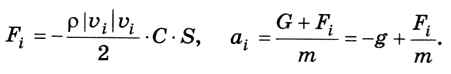
Предполагая, что мяч летел с постоянным ускорением a_i в течение всего интервала величиной 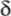, вычислим его скорость и координату в момент t_i+1 по формулам для равноускоренного движения:

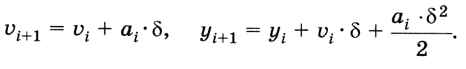
Эта дискретная модель описывает изменение скорости и высоты мяча через интервал .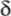

Следующая страница Компьютерная модель

Cкачать материалы урока