Урок 8
§6. Алгоритмические структуры

6.1. Последовательная алгоритмическая конструкция

Вне зависимости от выбранной формы записи элементарные шаги алгоритма объединяются в алгоритмические конструкции (структуры): последовательные, разветвляющиеся, циклические, вспомогательные и рекурсивные. Для записи любого алгоритма достаточно трёх основных алгоритмических структур: последовательной, разветвляющейся, циклической.

Алгоритм реализован через последовательную алгоритмическую конструкцию, если все команды алгоритма выполняются один раз, причём в том порядке, в котором они записаны в тексте программы.

Пример 1. Алгоритм, реализованный через последовательную алгоритмическую конструкцию, представлен блок-схемой на рисунке 2.4.

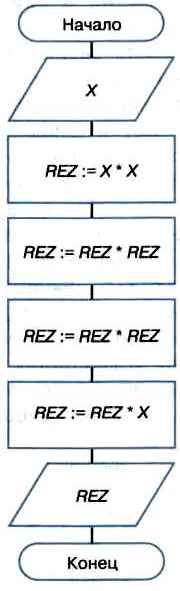
Рис. 2.4. Последовательная алгоритмическая конструкция

Выясните, какую задачу решает этот алгоритм. Чему равен результат работы алгоритма при х = 2?

Пример 2. Из курса информатики основной школы вам знаком исполнитель Вычислитель, выполняющий программы линейной структуры. Его система команд может содержать две и более команды с использованием арифметических операций.

Пусть исполнитель Вычислитель может выполнять следующие команды:

1) прибавь 2;
2) умножь на 3.

Подсчитаем, сколько разных программ, состоящих из трёх команд, можно составить для этого исполнителя, и выясним число различных значений, которые будут получены в результате их исполнения при начальном значении 2.

Так как каждую из команд вы можете выбрать одним из двух вариантов, а всего команд в программе три, общее число программ находится как N = 2³.

Для удобства поиска числа разных вариантов значений, которые будут получены по этим программам, составим дерево решений (рис. 2.5). В его корневой вершине (0-й уровень) записывается начальное значение. Ветви дерева соответствуют командам: левые — первой, правые — второй. В каждой вершине дерева 1-го, 2-го и т. д. уровней записывается результат, полученный после применения команды к числу из вершины-предка. Путь к каждой из вершин соответствует последовательности команд (программе) для получения значения, находящегося в вершине. Таким образом в вершинах N-го уровня будут записанны результаты программ, состоящих из N команд.

Cкачать материалы урока