Урок 8
§6. Алгоритмические структуры

6.1. Последовательная алгоритмическая конструкция (продолжение)

В нашем примере все значения в вершинах третьего уровня различны. Иногда значения в вершинах одного уровня совпадают. Можно сказать, что в общем случае число различных значений на уровне не превышает числа его вершин.

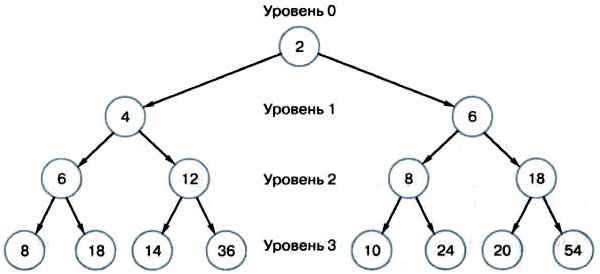
Рис. 2.5. Пример дерева решений

Номер уровня, на котором впервые появляется необходимое число, равен минимальному количеству команд для его получения. В нашем примере число 8 записано в вершинах 2-го и 3-го уровней, следовательно, минимальное количество команд для его получения равно двум.

Для определения количества программ, с помощью которых требуемое число получается из заданного, можно подсчитать количество вершин дерева, в которых записано требуемое число.

Подумайте, почему при заданных условиях существует только две программы для получения из числа 2 числа 8.

Если количество уровней вершин в дереве решений превышает четыре, то строить такое дерево неудобно. Так же как и в случае, когда система команд исполнителя состоит из трёх и более команд.

Для некоторых задач удобнее строить обратное дерево решений: команды исполнителя меняются на «обратные», пути строятся от результата к начальному значению.

На рисунке 2.6 показан пример построения обратного дерева решений (из числа 8 получаем число 2; команды: 1) вычти 2; 2) раздели на 3).

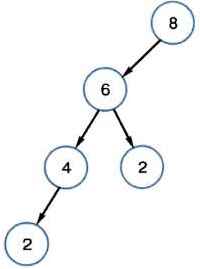
Рис. 2.6. Пример обратного дерева

Этот приём удобно использовать, когда обратные команды неприменимы ко всем решений вершинам.

Cкачать материалы урока