Урок 14
§9 (3, 4). Рекурсивные алгоритмы

9.3. Рекурсивные алгоритмы

Алгоритм называется рекурсивным, если на каком-либо шаге он прямо или косвенно обращается сам к себе.

Пример 2. Как известно, факториал натурального числа n определяется следующим образом: n! = 1 • 2 • 3 • ... • n; 0! считается равным единице (0! = 1).

Иначе это можно записать так:

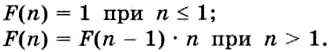
В определении факториала через рекурсию имеется условие n ≤ 1, при достижении которого вызов рекурсии прекращается.

В рекурсивном определении должно присутствовать ограничение (граничное условие), при выходе на которое дальнейшая инициация рекурсивных обращений прекращается.

Пример 3. Определим функцию S(n), вычисляющую сумму цифр в заданном натуральном числе n:

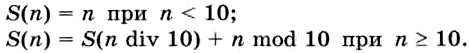
Самостоятельно определите функцию К(n), которая возвращает количество цифр заданного натурального числа n.

Пример 4. Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

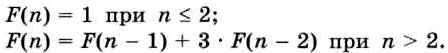
Требуется выяснить, чему равно значение функции F(7). По условию, F(1) = F(2) = 1.

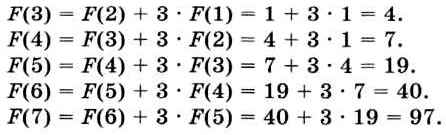
Подобные вычисления можно проводить в уме, а их результаты фиксировать в таблице:

Cкачать материалы урока