Урок 14
§9 (3, 4). Рекурсивные алгоритмы

9.3. Рекурсивные алгоритмы (продолжение)

Пример 5. Исполнитель Плюс имеет следующую систему команд:

1) прибавь 1;
2) прибавь 2;
3) прибавь 4.

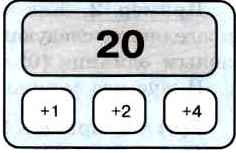
С помощью первой из них исполнитель увеличивает число на экране на 1, с помощью второй — на 2, с помощью третьей — на 4. Программа для исполнителя Плюс — это последовательность команд. Выясним, сколько разных программ, преобразующих число 20 в число 30, можно составить для этого исполнителя.

Количество программ, с помощью которых можно получить некоторое число n, будем рассматривать как функцию К(n).

Число, меньшее 20, при заданных начальных условиях и системе команд исполнителя Плюс получить невозможно. Следовательно, при n < 20 К(n) = 0.

Для начального числа 20 количество программ равно 1: существует только одна пустая программа, не содержащая ни одной команды. Можем записать: К(n) = 1 при n = 20.

Любое число n > 20 может быть получено из чисел n - 1, n - 2 и n - 4 одной из трёх команд, входящих в систему команд исполнителя — «прибавь 1», «прибавь 2» и «прибавь 4» соответственно. При этом каждая программа получения из исходного числа чисел n-1, n-2 и n-4 удлинится на одну команду и будет приводить к числу n. Следовательно, К(n) = К(n - 1) + + К(n - 2) + К(n - 4).

Запишем все соотношения, определяющие функцию К(n):

К(n) = 0 при n < 20;

К(n) — 1 при n = 20;

К(n) = К(n - 1) + К(n - 2) + К(n - 4) при n > 20.

Заполним по этой формуле таблицу для всех значений n от 20 до 30:

Итак, существует 169 различных программ, с помощью которых исполнитель Плюс может преобразовать число 20 в 30.

Любой объект, который частично определяется через самого себя, называется рекурсивным. Нас окружает множество рекурсивных объектов. Приведём примеры только некоторых из них.

1. Матрёшка — русская деревянная игрушка в виде расписной куклы, внутри которой находятся подобные ей куклы меньшего размера.

2. Два зеркала, поставленные друг напротив друга, — в них образуются два коридора из затухающих отражений. Это, например, можно наблюдать в спальном железнодорожном вагоне.

3. Примером рекурсивной структуры является замечательное стихотворение Р. Бернса «Дом, который построил Джек» в переводе С. Маршака.

4. Рекурсивную природу имеют геометрические фракталы. На рисунке представлено построение одного из геометрических фракталов — треугольника Серпинского. Чтобы его получить, нужно взять равносторонний треугольник с внутренней областью, провести в нём средние линии и «выкинуть» центральный из четырёх образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трёх треугольников, и т. д.

Cкачать материалы урока