Урок 14
§9 (3, 4). Рекурсивные алгоритмы

САМОЕ ГЛАВНОЕ

Структурное программирование — технология разработки программного обеспечения, в основе которой лежит представление программы в виде иерархической структуры логически целостных фрагментов (блоков).

Основные принципы структурного программирования заключаются в том, что:

1) любая программа строится из трёх базовых управляющих конструкций: последовательность, ветвление, цикл;
2) в программе базовые управляющие конструкции могут быть вложены друг в друга произвольным образом;
3) повторяющиеся фрагменты программы можно оформить в виде подпрограмм (процедур и функций). В виде подпрограмм можно оформить логически целостные фрагменты программы, даже если они не повторяются;
4) все перечисленные конструкции должны иметь один вход и один выход;
5) разработка программы ведётся пошагово, методом «сверху вниз».

Вспомогательный алгоритм — это алгоритм, целиком используемый в составе другого алгоритма.

Алгоритм называется рекурсивным, если на каком-либо шаге он прямо или косвенно обращается сам к себе.

Запись вспомогательных алгоритмов в языках программирования осуществляется с помощью подпрограмм. В языке Pascal различают два вида подпрограмм: процедуры и функции.

Вопросы и задания

1. В чём заключается сущность структурного программирования? Какие преимущества обеспечивает эта технология?

2. Какой алгоритм называется вспомогательным?

3. Вспомните, в чём состоит суть метода последовательного построения (уточнения) алгоритма. Как он называется иначе?

4. Опишите основные шаги разработки программы методом «сверху вниз».

5. Дан прямоугольный параллелепипед, длины рёбер которого равны а, b и с.

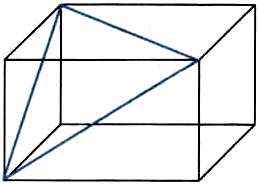
Требуется определить периметр треугольника, образованного диагоналями его граней. Какой алгоритм целесообразно использовать при решении этой задачи в качестве вспомогательного?

6. Какой вспомогательный алгоритм называется рекурсивным? Что такое граничное условие и каково его назначение в рекурсивном алгоритме?

7. Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

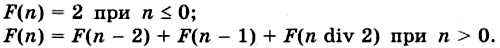
Требуется выяснить, чему равно значение функции F(10).

8. Исполнитель Калькулятор имеет следующую систему команд:

1) прибавь 1;
2) умножь на 2.

С помощью первой из них исполнитель увеличивает число на экране на 2, с помощью второй — в 2 раза.

1) Выясните, сколько разных программ, преобразующих число 1 в число 20, можно составить для этого исполнителя.
2) Сколько среди них таких программ, у которых в качестве промежуточного результата обязательно получается число 15?
3) Сколько среди них таких программ, у которых в качестве промежуточного результата никогда не получается число 12?

9. Попробуйте найти рекурсивные синтаксические структуры:

1) в поэме А. Блока «Двенадцать»;
2) в стихотворении М. Лермонтова «Сон»;
3) в романе М. Булгакова «Мастер и Маргарита»;
4) в фольклоре.

10. Найдите информацию о таких геометрических фракталах, как Снежинка Коха, Т-квадрат, Н-фрактал, кривая Леви, Драконова ломаная.

11. Напишите программу вычисления значения функции F(n), рассмотренной в примере 4 этого параграфа. Вычислите с её помощью значение функции F(7).

12. Напишите программу вычисления 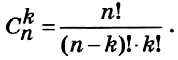Используйте подпрограмму.

13. Дана программа:

Не выполняя программу на компьютере, выясните, что получится в результате работы этой программы.

Проверьте свой результат, выполнив программу на компьютере.

Дополнительные материалы к главе смотрите в авторской мастерской.

Cкачать материалы урока