Урок 18
§11.2. Знакомство с теорией игр

САМОЕ ГЛАВНОЕ

Графы как информационные модели находят широкое применение во многих сферах нашей жизни. С их помощью можно планировать оптимальные транспортные маршруты, кратчайшие объездные пути, расположение торговых точек и других объектов.

Путь между вершинами А и В графа считается кратчайшим, если эти вершины соединены минимальным числом рёбер (в случае, если граф не является взвешенным) или если сумма весов рёбер, соединяющих эти вершины, минимальна (для взвешенного графа).

Для определения кратчайшего пути между вершинами графа используются алгоритм построения дерева решений, алгоритм Дейкстры, метод динамического программирования и другие алгоритмы.

Важную роль в решении многих задач экономики, социологии, политологии, биологии, искусственного интеллекта и ряда других областей, где необходимо изучение поведения человека и животных в различных ситуациях, играет теория игр.

Игра, выступающая в качестве математической модели некоторой ситуации, характеризуется такими признаками, как:

1) присутствие нескольких игроков;
2) неопределённость поведения игроков, связанная с имеющимися у каждого из них несколькими вариантами действий;
3) различие (несовпадение) интересов игроков;
4) взаимосвязанность поведения игроков (результат, получаемый каждым из них, зависит от поведения всех игроков);
5) наличие правил поведения, известных всем игрокам.

Игра может быть представлена в виде дерева, каждая вершина которого соответствует ситуации выбора игроком своей стратегии.

В играх с полной информацией участники знают все ходы, сделанные до текущего момента, равно как и возможные стратегии противников, что позволяет им в некоторой степени предсказать последующее развитие игры.

Выигрышная стратегия — это правило, следуя которому игрок выигрывает независимо от того, как играет противник.

Вопросы и задания

1. В решении каких прикладных задач используются алгоритмы нахождения кратчайшего пути между заданными вершинами в графе?

2. С помощью алгоритма Дейкстры найдите кратчайший путь между вершинами А и G следующего графа:

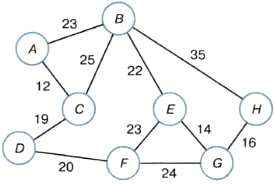
В материалах международного конкурса по информатике «Бобёр» есть такая задача, предложенная разработчиками из Нидерландов.

Бобёр Билли любит жёлуди. Он хочет поплыть по течению и собрать все жёлуди на островах, мимо которых будет проплывать. Увы, течение реки настолько сильное, что он может плыть только вниз по течению. Какое максимальное количество желудей он сможет собрать?

Решите эту задачу, воспользовавшись методом динамического программирования.

4. На столе лежит 25 спичек. Играют двое. Игроки по очереди могут взять от одной до четырёх спичек. Кто не может сделать ход (т. к. спичек не осталось), проигрывает. Другими словами, выигрывает взявший последнюю спичку. Выясните, у кого из игроков есть выигрышная стратегия.

5. Выясните, у кого из двух игроков есть выигрышная стратегия в такой игре: начальная позиция — на столе лежит 107 спичек, за один ход можно брать 1 или 2 спички. Выигрывает тот, кто взял последнюю спичку.

6. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 2, во второй — 3 камня. У каждого игрока неограниченное количество камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает число камней в какой-то куче в 3 раза, или добавляет 3 камня в любую из куч. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 35. Кто выигрывает — игрок, делающий ход первым, или игрок, делающий ход вторым?

7. Два игрока, Петя и Ваня, играют в следующую игру¹⁾. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу 1 камень или 5 камней. Например, имея кучу из 10 камней, за один ход можно получить кучу из 11 или 15 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 47. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет 47 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 46. Выполните следующие задания, в каждом случае обосновывая свой ответ.

1) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения Б, и укажите выигрывающие ходы.
2) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
3) Укажите два значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть за один ход, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанных значений S опишите выигрышную стратегию Пети.
4) Укажите значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, однако у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани.

---

¹⁾ Большое количество подобных заданий вы можете найти в открытом банке заданий ЕГЭ по информатике на сайте fipi.ru.

Cкачать материалы урока