Уроки 2 - 7
§1.2. Построение и исследование физических моделей

Содержание урока

1.2.1. Построение формальной модели движения тела, брошенного под углом к горизонту

Содержательная постановка задачи «Бросание мячика в стенку»

Описательная модель

Формальная модель

Контрольные вопросы

1.2.2. Компьютерная модель движения тела на языке Visual Basic

1.2.3. Компьютерная модель движения тела на языке Turbo Delphi

1.2.4. Компьютерная модель движения тела в электронных таблицах

1.2.1. Построение формальной модели движения тела, брошенного под углом к горизонту

Формальная модель

Для формализации модели обозначим величины:

• начальную скорость мячика — V_o;
• угол бросания мячика — α;
• высоту стенки — h;
• расстояние до стенки — s.

Изобразим график движения мячика (рис. 1.1).

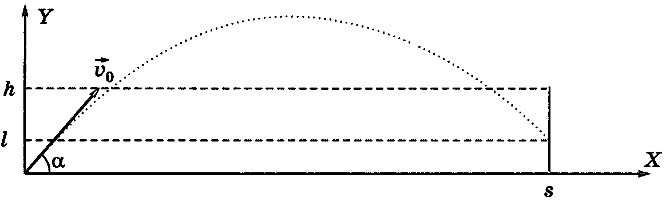
Рис. 1.1. Бросание мячика в стенку

Используем известные из курса физики формулы равномерного и равноускоренного движения для определения координат мячика.

Дальность х и высоту y при заданной начальной скорости V_o и угле бросания α для любого момента времени t можно вычислить по формулам:

х = V_o • cosα • t, y = V_o • sinα • t - g- t²/2.               (1.1)

Чтобы определить, попадет ли мячик в стенку, необходимо вычислить его координату у в момент времени, когда он будет находиться на расстоянии s. Из первой формулы выражаем время, которое понадобится мячику, чтобы преодолеть расстояние s:

t = s/V_o • cosα.

Подставляем это значение времени t в формулу для вычисления координаты y. Получаем I — высоту мячика над землей на расстоянии s (см. рис. 1.1):

I = s • tgα - g • s²/2 • V²_o • cos²α.               (1.2)

Формализуем теперь условие попадание мячика в мишень. Попадание произойдет, если значение высоты мячика I будет удовлетворять условию в форме неравенства:

0 ≤ I ≤ h.

Если I < 0, то это означает «недолет», а если I > А, то это означает «перелет».

Следующая страница Контрольные вопросы

Cкачать материалы урока