Урок 52
§29. Оптимизация
Содержание урока
Локальные и глобальный минимумы
Пример: оптимальная раскройка листа
Поиск оптимального решения с помощью электронных таблиц
Практическая работа №30 «Оптимизация»
Локальные и глобальный минимумы
По традиции обычно рассматривают задачу поиска минимума. Если нужно найти максимум, просто меняют знак функции: значение функции f(x) максимально там, где значение функции -f(x) минимально.
В математике различают локальный («местный») и глобальный («общий») минимум (рис. 5.18).
 Локальный минимум — минимальное значение функции в окрестности некоторой точки.
Локальный минимум — минимальное значение функции в окрестности некоторой точки.
 Глобальный минимум — минимальное значение функции при заданных ограничениях.
Глобальный минимум — минимальное значение функции при заданных ограничениях.
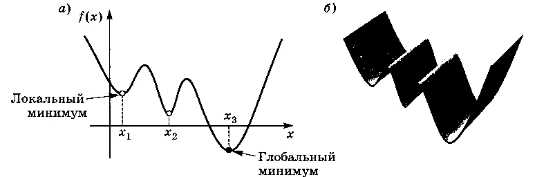
Рис. 5.18
Минимум в точке х3 — глобальный, потому что здесь функция имеет наименьшее значение во всей рассматриваемой области.
Очевидно, что нас всегда интересует глобальный минимум. Однако большинство существующих методов оптимизации 1) предназначены именно для поиска локальных минимумов вблизи заданной начальной точки (начального приближения).
1) Для некоторых типов функций существуют методы глобальной оптимизации, но они сложны и выходят за рамки школьного курса.
Можно представить себе, что график функции — это срез поверхности, на которую устанавливается шарик в некоторой начальной точке (см. рис. 5.18, б); куда этот шарик скатится, такой минимум и будет найден.
Результат поиска локального минимума зависит от начального приближения.
Следующая страница  Пример: оптимальная раскройка листа
Пример: оптимальная раскройка листа

