Урок 52
§29. Оптимизация

Содержание урока

Что такое оптимизация?

Локальные и глобальный минимумы

Пример: оптимальная раскройка листа

Поиск оптимального решения с помощью электронных таблиц

Выводы

Вопросы и задания

Практическая работа №30 «Оптимизация»

Практическая работа №30 «Оптимизация»

Уровень A. Определите, на какой минимальный срок (целое число лет) необходимо поместить в банк 20000 руб., чтобы получить не менее 100000 при 10% годовых.

Уровень B. Найдите стороны прямоугольного треугольника, имеющего наибольшую возможную площадь, если известно, что сумма длин его катетов равна 10.

Уровень C. На кондитерской фабрике выпускаются конфеты трёх сортов. Известны расходы компонентов (в граммах) на 1 кг каждого сорта и общие запасы, имеющиеся на складе:

Установлены такие цены за 1 кг: конфеты «Гвоздика» – 180 рублей, «Романтика» – 200 рублей и «Карнавал» – 170 рублей. Сколько килограммов конфет каждого сорта нужно выпустить, чтобы доход фабрики была наибольший?

Уровень D. В посёлке построили четыре многоэтажных дома, и теперь нужно выбрать место для строительства магазина так, чтобы сумма расстояний от всех домов до магазина была минимальной. Известны координаты домов в прямоугольной системе координат (x, y).

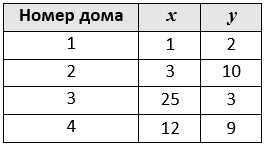
Определите координаты магазина. Подсказка: для вычисления расстояния между домом и магазином нужна функция SQRT (КОРЕНЬ).

Следующая страница §29. Оптимизация

Cкачать материалы урока