Уроки 44 - 45
Практическая работа 2.3
«Выполнение геометрических построений в системе компьютерного черчения КОМПАС»

Содержание урока

Аппаратное и программное обеспечение

Задание 2.3.1. Геометрическое построение угла, равного заданному

Задание 2.3.2. Построение треугольника по двум сторонам и углу между ними

Задание 2.3.3. Построение треугольника по трем сторонам

Задание 2.3.4. Построение перпендикуляра к заданной прямой

Задание 2.3.5. Построение биссектрисы неразвернутого угла

Задание 2.3.5. Построение биссектрисы неразвернутого угла

Формальная модель. Построим формальную модель процесса геометрического построения, зафиксировав его в форме алгоритма.

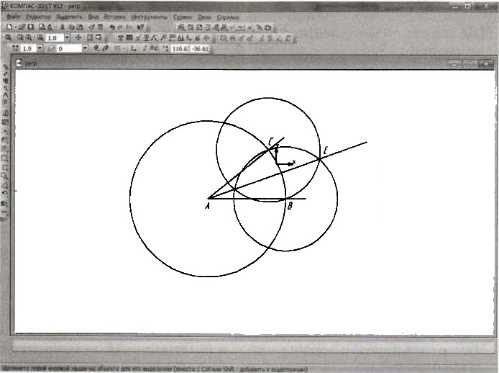
1) Построить окружность произвольного радиуса с центром в вершине заданного угла А, которая пересечет стороны угла в точках В и С.
2) Построить две окружности радиуса ВС с центрами в точках В и С. Точку пересечения окружностей внутри угла обозначить буквой Е.
3) Через вершину угла А и точку пересечения окружностей Е провести прямую. Отрезок АЕ — биссектриса заданного угла.

Начертим геометрические объекты, заданные в условии задачи: два отрезка, исходящих из одной точки под произвольным неразвернутым углом.

1. Построить два отрезка, исходящие из одной точки. Ввести обозначение угла на чертеже «А».

Построим окружность произвольного радиуса с центром в вершине заданного угла А.

2. Построить окружность произвольного радиуса с центром в точке А.

3. С помощью Компактной панели вызвать панель Обозначения. Щелкнуть по кнопке Ввод текста и обозначить точки пересечения сторон угла и окружности буквами В и С.

Построим две окружности радиуса ВС с центрами в точках В и С.

4. На панели Геометрия выбрать объект Окружность.

Построим окружность радиуса, равного отрезку ВС, с центром в точке В. Для этого на Панели свойств щелкнуть правой кнопкой мыши по полю Радиус и в контекстном меню выбрать пункт Между 2 точками.

На чертеже навести курсор сначала на точку В, а затем — на точку С.

Центр появившейся окружности заданного радиуса переместить в точку В.

Аналогично построить окружность радиуса, равного длине отрезка ВС, с центром в точке С.

5. Точку пересечения окружностей обозначить Е.

Через вершину угла А и точку пересечения окружностей Е проведем прямую.

6. Начертить отрезок через точки А и В. Отрезок АЕ — биссектриса заданного угла.

Cкачать материалы урока