Уроки 2 - 3
Информатика и информация. Информационные процессы. Измерение информации
§1. Информатика и информация. §2. Что можно делать с информацией? §3. Измерение информации
Содержание урока
§1. Информатика и информация
§2. Что можно делать с информацией?
§3. Измерение информации
Что такое бит?
§3. Измерение информации
Что такое бит?
Рассмотрим электрическую лампочку, которая может находиться в двух состояниях: «горит» и «не горит». Тогда на вопрос «Горит ли сейчас лампочка» есть два возможных варианта ответа, которые можно обозначить цифрами 1 («горит») и 0 («не горит») (рис. 1.5). Поэтому ответ на этот вопрос (полученная информация) может быть записан как 0 или 1 1.
1 Конечно, вместо 0 и 1 можно использовать два любых знака.
Цифры 0 и 1 называют двоичными, и с этим связано название единицы измерения количества информации — бит. Английское слово bit — это сокращение от выражения binary digit — «двоичная цифра». Впервые слово «бит» в этом значении использовал американский инженер и математик Клод Шеннон в 1948 г.
Бит — это количество информации, которую можно записать (закодировать) с помощью одной двоичной цифры.
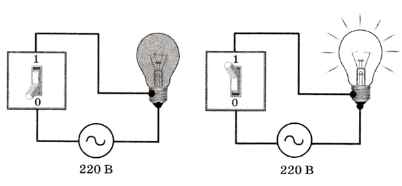
Рис. 1.5
Конечно, нужно договориться, что означают 0 и 1 (1 — это «горит» или «не горит»?), но для измерения количества информации это не важно.
Например, в сообщении «подброшенная монета упала гербом» содержится 1 бит информации, потому что монета могла упасть гербом (обозначим это через 0) или «решкой» (1). Сообщение «Дверь открыта» тоже содержит 1 бит, если считать, что дверь может быть в двух состояниях: открыта (0) или закрыта (1). Вот ещё пример диалога, в котором получена информация в 1 бит:
— Вы будете чай или кофе?
— Кофе, пожалуйста.
2 бита, 3 бита...
А если возможных вариантов не два, а больше? Понятно, что в этом случае количество информации будет больше, чем 1 бит. Представим себе, что на вокзале стоят 4 одинаковых поезда (рис. 1.6), причём только один из них проследует в Москву. Сколько битов понадобится для того, чтобы записать информацию о номере платформы, где стоит поезд на Москву?
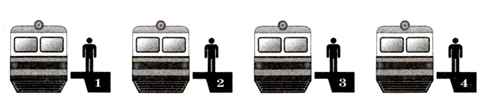
Рис. 1.6
Очевидно, что одного бита недостаточно, так как с помощью одной двоичной цифры можно закодировать только два варианта — коды 0 и 1. А вот два бита дают как раз 4 разных сообщения: 00, 01, 10 и 11. Теперь нужно сопоставить эти коды номерам платформ, например, так: 1 — 00, 2 — 01, 3 — 10, 4 — 11. Тогда сообщение 10 говорит о том, что поезд на Москву стоит на платформе № 3. Это сообщение несёт 2 бита информации.
Три бита дают уже 8 вариантов: 000, 001, 010, 011, 100, 101, 110 и 111. Таким образом, каждый бит, добавленный в сообщение, увеличивает количество вариантов в 2 раза (табл. 1.1).
Наверно, вы заметили, что все числа в нижней строчке таблицы — это степени числа 2: N = 2I.
Осталось выяснить, чему равно количество информации, если выбор делается, скажем, из 5 возможных вариантов (или из любого количества, не являющегося степенью числа 2). С точки зрения приведённого выше рассуждения случаи выбора из 5, 6, 7 и 8 вариантов не различаются — для кодирования двух двоичных цифр мало, а трёх — достаточно. Поэтому использование трёх битов для кодирования одного из 5 возможных вариантов избыточно, ведь три бита позволяют закодировать целых 8 вариантов! Значит, выбор из 5 вариантов даёт меньше трёх битов информации.
Чтобы количественно измерить разницу между, скажем, 5 и 8 вариантами, придется допустить, что количество информации в битах может быть дробным числом. При этом информация, полученная при выборе из 5 вариантов, больше, чем 2 бита, но меньше, чем 3 бита. Точную формулу для ее вычисления получил в 1928 г. американский инженер Ральф Хартли. Эта формула использует понятие логарифма, поэтому мы познакомимся с ней в 11 классе.
Тем не менее уже сейчас вы можете оценить количество информации при выборе из 5 вариантов. Допустим, на завтрак в лагере отдыха каждый день дают кашу одного из 5 видов. Чтобы закодировать вид каши, которую дают в понедельник, нужно, как мы знаем, 3 бита. Но меню на два дня может быть составлено 25 разными способами (5 • 5), поэтому для его кодирования достаточно 5 битов, ведь 25 < 32 = 25! Тогда получается, что количество информации при выборе информации из 5 вариантов меньше, чем 5/2 = 2,5 бита. Но и эту оценку можно уточнить. Для трёх дней получаем 5 • 5 • 5 = 125 вариантов. Так как 125 < 128 = 27, количество информации при выборе из 5 вариантов составляет не больше, чем 7/3 = 2,33 бита. И так далее. Попробуйте самостоятельно показать, что при выборе из 5 вариантов количество информации больше 2,25 бита. Верно ли, что при выборе из 6 вариантов количество информации менее 2,5 бита?
Следующая страница 
Другие единицы
Cкачать материалы урока
