Уроки 121 - 122
Восстановление зависимостей в табличных процессорах
§74. Обработка результатов эксперимента
Содержание урока
Метод наименьших квадратов
Метод наименьших квадратов
Предположим, что есть два ряда данных одинаковой длины: х1,х2,...,хn и y1,y2,...,yn. Предполагается, что они связаны линейной зависимостью y = k • x, где k — неизвестный коэффициент. Требуется найти оптимальное значение k, которое лучше всего соответствует исходным данным.
Поскольку речь идёт о задаче оптимизации, нужно определить функцию, которая позволяет оценить, насколько хорошо выбранная зависимость соответствует исходным данным. Предположим, что выбран некоторый коэффициент k, так что для каждого xz можно найти соответствующее ему значение функции Yi = k • xi.
В идеале график функции должен проходить через все точки (x1, y1), (x2,y2), ...» (хn,yn), т. е. при всех i должно выполняться условие Yi = yi. Однако на практике этого, скорее всего, не будет (рис. 9.27).
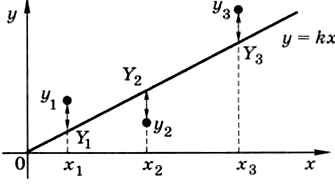
Рис. 9.27
Отклонение полученной линии от исходных данных определяется разностями Yi - yi: чем они меньше (по модулю), тем лучше соответствие. Однако сумма этих разностей даёт неправильную оценку точности — слагаемые с разными знаками могут скомпенсировать друг друга. Чтобы решить эту проблему, можно сложить квадраты этих величин и выбрать k так, чтобы эта сумма
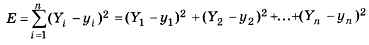
была минимальной. Такой подход называется методом наименьших квадратов. Впервые его предложил немецкий математик К. Ф. Гаусс.
Как найти коэффициент k наилучшим образом, т. е. так, чтобы сумма квадратов Е была минимальной? Для этого заменим Yi на k • xi и раскроем скобки в формуле для вычисления Е:
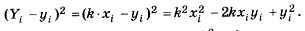
Группируя слагаемые, содержащие k2 и k, получаем:
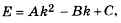
где 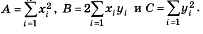 График зависимости E от k — это парабола, причём её ветви направлены вверх, потому что
А > 0 (это сумма квадратов). Вершина параболы (и минимум функции!) находится в точке k = B/2А, это и будет оптимальное решение.
График зависимости E от k — это парабола, причём её ветви направлены вверх, потому что
А > 0 (это сумма квадратов). Вершина параболы (и минимум функции!) находится в точке k = B/2А, это и будет оптимальное решение.
Таким образом, алгоритм для определения оптимального значения k приобретает вид:
1) вычислить коэффициенты параболы 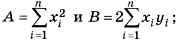
2) вычислить k = B/2А
Решение получилось простым только потому, что мы выбрали очень простую функцию, линейную с нулевым свободным членом. В более сложных случаях строгое решение задачи оптимизации требует знания высшей математики.
Если исходные данные записаны в массивах х[1..N] и y[1..N], программа для рассмотренного случая выглядит так:
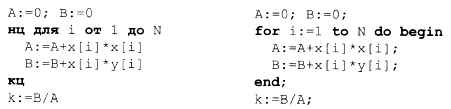
Чтобы избавиться от лишних операций, умножение на 2 при вычислении В и деление на 2 при вычислении k не выполняется (применение двух этих операций не меняет результат).
Для решения задачи методом наименьших квадратов можно использовать табличные процессоры с модулем поиска решения. Пусть в результате измерений получены точки (1; 1,1), (2; 1,8) и (3; 3,5). Занесём эти координаты в столбцы А и В, в ячейку В1 запишем начальное приближение для к, а в столбец С — значения функции y = k • х для значений х из столбца А (рис. 9.28).
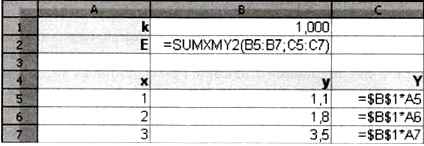
Рис. 9.28
Величина Е — это сумма квадратов разностей двух рядов, которая вычисляется с помощью функции SUMXMY2 (СУММКВРАЗН). У этой функции два аргумента — ряд у (измеренные значения в столбце В) и ряд У (вычисленные значения функции в столбце С). Задача оптимизации — найти минимальное значение Е (в ячейке В2), изменяя значение k в ячейке В1 — решается с помощью надстройки «Поиск решения».
Следующая страница  Восстановление зависимостей
Восстановление зависимостей

