Уроки 121 - 122
Восстановление зависимостей в табличных процессорах
§74. Обработка результатов эксперимента

Содержание урока

Зачем это нужно?

Метод наименьших квадратов

Восстановление зависимостей

Прогнозирование

Вопросы и задания

Задачи

Восстановление зависимостей

Пусть заданы пары значений х и y, и предполагается, что они связаны некоторой зависимостью у = f(x), которую нужно найти для того, чтобы вычислять значение функции в других точках, для которых значения у неизвестны. Такая задача называется задачей восстановления зависимости.

Если вид функции не задан, эта задача некорректна, потому что через заданные точки можно провести сколько угодно различных линий (графиков функций), и невозможно сказать, какая из них лучше подходит (рис. 9.29).

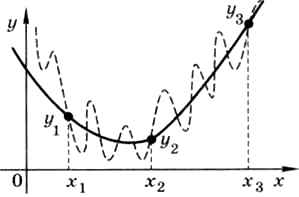
Рис. 9.29

Поэтому для того, чтобы сделать задачу осмысленной, нужно заранее задать вид функции, так что останется только найти её неизвестные коэффициенты.

Откуда взять вид функции? В некоторых случаях он известен из физических законов, описывающих явление (так было в примере с исследованием закона Гука). Иногда вид зависимости можно определить по внешнему виду расположения точек. Также можно попробовать функции разного типа и выбрать лучший вариант. Часто используют следующие типы функций (рис. 9.30):

• линейную y = а • х + b;
• логарифмическую у = а • ln х + b;
• показательную (экспоненциальную) y = а • b^х;
• степенную y =а • х^b.

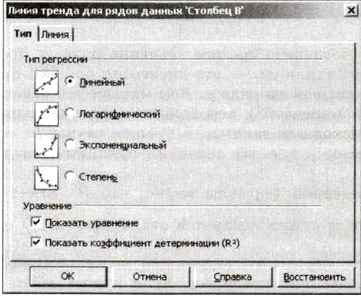
Рис. 9.30

Задача сводится к тому, чтобы выбрать коэффициенты а и b наилучшим образом. Для её решения «вручную» нужно применять методы вычислительной математики, выходящие за рамки школьного курса. Однако в современных табличных процессорах есть встроенные возможности для решения задачи восстановления зависимостей. Полученные графики оптимальных функций называются линиями тренда (англ, trend — основное направление развития).

Сначала нужно ввести исходные данные (координаты точек) в таблицу и построить по ним диаграмму типа Диаграмма ХY (в Excel — диаграмма Точечная). Лучше оставить на диаграмме только точки, не соединяя их линией.

Для того чтобы построить линию тренда, надо щёлкнуть правой кнопкой мыши на одной из точек и выбрать пункт Вставить линию тренда из контекстного меню. В появившемся окне можно выбрать вид зависимости. Если установить флажок Показать уравнение, уравнение линии тренда будет показано на диаграмме. Флажок Показать коэффициент детерминации (R²) позволяет увидеть, насколько точно полученная линия соответствует исходным данным. Коэффициент R² вычисляется по формуле

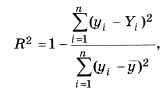
где через y обозначено среднее значение ряда y. Дробь, которая вычитается из единицы, — это дисперсия ошибки приближения, делённая на дисперсию ряда y. Чем меньше это отношение (и чем больше коэффициент R²), тем больше найденная зависимость соответствует исходным данным. В лучшем случае R² = 1, при этом y_i = Y_i для всех i , т. е. все значения функции совпадают с заданными.

Из приведённой формулы видно, что R² имеет наибольшее значение, когда сумма квадратов отклонений 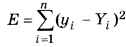нимальна. Это значит, что задача поиска максимума R² решается методом наименьших квадратов. Если нужно найти неизвестные коэффициенты функции, которая не входит в стандартный набор (например, y = a • sinbx + c), можно применить метод наименьших квадратов с помощью надстройки «Поиск решения».

Следующая страница Прогнозирование

Cкачать материалы урока