Урок 36
Выполнение арифметических операций с нормализованными числами
§30. Операции с вещественными числами

Содержание урока

Сложение и вычитание

Умножение и деление

Вопросы и задания

Задачи

Сложение и вычитание

Рассмотрим принципы вещественной компьютерной арифметики на простых примерах. Сложим 7,25₁₀ = 111,01 и 1,75₁₀ = 1,11 (здесь и далее будем явно указывать систему счисления только для десятичных чисел). Представим эти числа в нормализованном виде: 111,01 • 2⁰ = 1,1101 • 2¹⁰ и 1,11 • 2⁰ (ещё раз подчеркнём, что значащие части и порядки чисел указываются в двоичной системе!). Не будем сейчас использовать «скрытую» единицу: это нужно только при сохранении чисел в памяти, а при изучении арифметических действий удобнее иметь «развёрнутые» значения.

Числа, записанные в форме с плавающей запятой, нельзя непосредственно сложить. Дело в том, что когда числа имеют разные порядки, их значащие части оказываются сдвинутыми друг относительно друга. Поэтому первое, что делает процессор перед сложением вещественных чисел, — выравнивает их порядки до большего. Число, имеющее меньший порядок р₂ (и значащую часть z₂), «подгоняется» к числу с большим порядком р₁ следующим образом:

1. Если р₂ = p₁, то порядки выровнены и преобразования закончены.

2. p₂ = p₂ + 1.

3. Сдвинуть значащую часть z₂ на один разряд вправо.

4. Перейти к шагу 1.

Для нашего примера разность порядков равна 10 - 0 = 10 = 2₁₀, так что для выравнивания порядков значащую часть придётся сдвинуть дважды (порядок при этом увеличится на 2): 1,11 • 2⁰ = 0,0111 • 2¹⁰. Подчеркнём, что ради проведения сложения нормализацию пришлось временно нарушить.

Теперь числа имеют одинаковый порядок и их значащие части можно складывать:

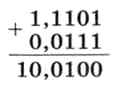
Полный результат (с учётом порядка) равен 10,01 • 2¹⁰ (убедитесь, что получившееся число равно 9₁₀). Но значащая часть результата больше 2, поэтому для записи числа в память его необходимо нормализовать: 10,01 • 2¹⁰ = 1,001 • 2¹¹.

В этом примере мы нигде не учитывали ограниченность разрядной сетки и для простоты специально взяли короткие числа. Как же обстоит дело в реальных вычислениях? При выравнивании порядков происходит сдвиг значащей части меньшего из чисел вправо, при этом ее младшие (правые) разряды могут выйти за пределы разрядной сетки и будут отброшены. При сложении чисел с большой разностью порядков в результате таких сдвигов меньшее число может стать равно нулю. Например, представьте себе, что при 24-битной значащей части у слагаемых А и В разность порядков составляет, например, 26₁₀. В этом случае при выравнивании порядков произойдёт 26 сдвигов значащей части вправо, так что абсолютно все(!) её разряды исчезнут. В результате сложения окажется, что А + В = А, хотя В ≠ 0 — это очередной (но далеко не единственный) пример погрешности компьютерных вычислений.

Следующая страница Умножение и деление

Cкачать материалы урока