Урок 6
Системы счисления. Позиционные системы счисления. Двоичная система счисления
§9. Системы счисления. §10. Позиционные системы счисления. §11. Двоичная система счисления
Содержание урока
§9. Системы счисления
§10. Позиционные системы счисления
§11. Двоичная система счисления
Дробные числа
§11. Двоичная система счисления
Дробные числа
Для перевода дробного числа в двоичную систему используется общий подход, описанный в § 10. В данном случае нужно умножать число на 2, запоминать целую часть и отбрасывать её перед следующим умножением. Например, для числа 0,8125 получаем табл. 2.4.
Таким образом, 0,8125 = 0,11012.
Давайте посмотрим, как хранится в памяти число 0,6. Выполняя умножение на 2 и выделение целой части, мы получим периодическую бесконечную дробь:
0,6 = 0,1001100110012... = 0,(1001)2.
Это значит, что для записи десятичного числа 0,6 в двоичной системе счисления требуется бесконечное число разрядов. Поскольку реальный компьютер не может иметь бесконечную память, число 0,6 в двоичном представлении хранится в памяти с ошибкой 1 (погрешностью).
1 Последний стандарт кодирования вещественных чисел IEEE 754-2008 позволяет записывать в память числа в десятичном виде. Однако вычисления с такими данными сложнее и медленнее, чем с двоичными. Кроме того, проблема конечного числа разрядов остаётся: десятичная дробь, равная 1/3, по-прежнему не может быть точно представлена в памяти компьютера.
Большинство дробных чисел хранится в памяти с некоторой погрешностью. При выполнении вычислений с дробными числами погрешности накапливаются и могут существенно влиять на результат.
Отметим, что эта проблема связана не с двоичной системой, а с ограниченным размером ячейки памяти компьютера, отведённой на хранение числа. В любой системе счисления существуют бесконечные дроби, которые не могут быть точно представлены конечным числом разрядов.
Обеспечение точности расчётов с дробными (вещественными) числами — это очень важная и актуальная проблема, пока до конца не решённая. Поэтому сначала надо попытаться решить задачу, используя только операции с целыми числами. Например, пусть требуется определить, верно ли, что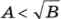 
, где А и В — целые неотрицательные числа. При извлечении квадратного корня мы сразу переходим в область вещественных чисел, где могут возникнуть вычислительные ошибки.
Вместо этого можно возвести обе части неравенства в квадрат и проверять равносильное условие А2 < В, используя только операции с целыми числами.
Если же всё-таки нужно обязательно использовать дробные числа и нельзя жертвовать точностью, приходится хранить их в нестандартном виде, например в виде отношения целых чисел (например, 0,6 = 6/10), и вычислять отдельно числители и знаменатели простых дробей, переходя к вещественным числам только при выводе конечного результата. Этот подход применяется в системах символьных вычислений, например в программных системах Maple (www.maplesoft.com) и Mathematica (www.wolfram.com). Однако выполнение таких расчётов занимает очень много времени.
Следующая страница 
Выводы
Cкачать материалы урока
