Уроки 17 - 18
Логика и компьютер. Логические операции. Диаграммы Эйлера-Венна
§18. Логика и компьютер. §19. Логические операции. §20. Диаграммы
Содержание урока
§18. Логика и компьютер
§19. Логические операции
Операция «И»
§20. Диаграммы
§19. Логические операции
Операция «И»
Пусть есть два высказывания: А — «Сейчас идёт дождь», В — «Форточка открыта». Сложное высказывание «А И В» выглядит так: «Сейчас идёт дождь и форточка открыта». Оно будет истинным в том и только в том случае, когда оба высказывания А и В истинны одновременно.
Для понимания операции «И» можно представить себе простую схему, в которой для включения лампочки используются два выключателя, соединённых последовательно (рис. 3.2).
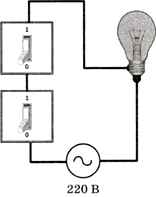
Рис. 3.2
Чтобы лампочка загорелась, нужно обязательно включить оба выключателя. Вместе с тем, чтобы выключить лампочку, достаточно выключить любой из них.
Операция «И» (в отличие от «НЕ») выполняется с двумя логическими значениями, которые мы обозначим как А и В.
Результат этой операции в алгебре логики записывают как А • В, А ∧ В или А & В. В языках программирования используют обозначения, такие как A and В (Паскаль, Бейсик), А && В (Си).
В таблице истинности (рис. 3.3) будет уже не один столбец с исходными данными, а два. Число строк также выросло с 2 до 4, поскольку для 2 битов (А и В) мы получаем 4 разных комбинации значений: 00, 01, 10 и 11. Эти строки расположены в определённом порядке: двоичные числа, полученные соединением значений А и В, идут в порядке возрастания (слева от таблицы на рис. 3.3 они переведены в десятичную систему). Как следует из определения операции, в последнем столбце будет всего одна единица, для варианта А = В = 1.
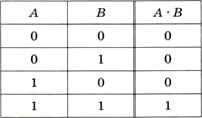
Рис. 3.3
Легко проверить, что этот результат можно получить «обычным» умножением А на В, поэтому операцию «И» называют логическим умножением. Кроме того, с точки зрения обычной математики, эта операция выбирает минимальное из исходных значений. Существует ещё одно название операции «И» — конъюнкция (лат. conjunctio — союз, связь).
Следующая страница  Операция «ИЛИ»
Операция «ИЛИ»

