Уроки 17 - 18
Логика и компьютер. Логические операции. Диаграммы Эйлера-Венна
§18. Логика и компьютер. §19. Логические операции. §20. Диаграммы
Содержание урока
§18. Логика и компьютер
§19. Логические операции
Импликация
§20. Диаграммы
§19. Логические операции
Импликация
Мы часто используем логическую связку «если..., то», например: «Если пойдёт дождь, то я надену плащ» или «Если все стороны прямоугольника равны, то это квадрат». В логике эта связка называется импликацией1 (следованием) и обозначается стрелкой: А → В («если А, то В», «из А следует В»). Таблица истинности операции импликации показана на рис. 3.8.
1 От лат. implicatio — сплетение, тесная связь.
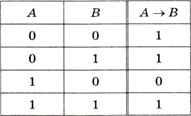
Рис. 3.8
Разобраться с импликацией будет легче, если мы рассмотрим конкретное высказывание, например, такое: «Если хорошо работаешь, то получаешь большую зарплату». Обозначим буквами два простых высказывания: А — «Вы хорошо работаете» и В — «Вы получаете большую зарплату». Понятно, что если высказывание А → В истинно, то все, кто хорошо работают (А = 1), должны получать большую зарплату (В = 1). Если же кто-то работает хорошо (А = 1), а получает мало (В = 0), то высказывание А → В ложно.
Лодыри и бездельники (А = 0) могут получать как маленькую (В = 0), так и большую зарплату (В = 1), это не нарушает истинность высказывания А → В. Иногда, определяя импликацию, говорят так: из истины следует истина, а из лжи — что угодно. Это значит, что при ложном высказывании А высказывание В может быть как ложно, так и истинно.
Нужно обратить внимание на разницу между высказываниями вида «если А, то В» в обычной жизни и в алгебре логики. В быту мы чаще всего имеем в виду, что существует причинно- следственная связь между А и В, т. е. именно А вызывает В. Алгебра логики не устанавливает взаимосвязь явлений; истинность высказывания А → В говорит только о возможности такой связи. Например, с точки зрения алгебры логики может быть истинным высказывание «Если Вася — студент, то Петя — лыжник».
Импликация чаще всего используется при решении логических задач, так как формулировку вида «если А, то В» можно записать как А → В = 1.
Для импликации (в отличие от других изученных ранее операций с двумя переменными) не действует переместительный закон: если в записи А → В поменять местами А и В, то результат изменится: А → В ≠ В → А. Внешне это видно по стрелке, которая указывает «направление».
Импликацию можно заменить на выражение, использующее только базовые операции (здесь — только «НЕ» и «ИЛИ»):
А → В = А + В.
Доказать это равенство вы уже можете самостоятельно.
Следующая страница  Эквивалентность
Эквивалентность

