Уроки 17 - 18
Логика и компьютер. Логические операции. Диаграммы Эйлера-Венна
§18. Логика и компьютер. §19. Логические операции. §20. Диаграммы
Содержание урока
§18. Логика и компьютер
§19. Логические операции
Операция «исключающее ИЛИ»
§20. Диаграммы
§19. Логические операции
Операция «исключающее ИЛИ»
Операция «исключающее ИЛИ» отличается от обычного «ИЛИ» только тем, что её результат равен 0, если оба значения равны 1 (последняя строка в таблице истинности). То есть результат этой операции — истина в том и только в том случае, когда два значения не равны (рис. 3.6).
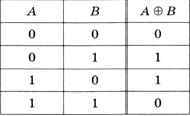
Рис. 3.6
Операции «исключающее ИЛИ» соответствует русская пословица «Либо пан, либо пропал», где выполнение обоих условий одновременно невозможно. Операция «исключающее ИЛИ» в алгебре логики обозначается знаком ⊕, в языке Паскаль — хоr (А хоr В), а в языке Си — знаком ^ (А ^ В). Эту операцию можно представить через базовые операции (НЕ, И, ИЛИ) следующим образом:
А ⊕ В = А • В + А • В.
Пока мы не можем вывести это равенство, но можем доказать его (или опровергнуть, т. е. доказать, что оно неверное). Для этого достаточно для всех возможных комбинаций А и В вычислить значения выражения, стоящего в правой части равенства, и сравнить их со значениями выражения А ⊕ В для тех же исходных данных. Поскольку провести такие вычисления в уме достаточно сложно, сначала вычислим значения А, В, А • В и А • В, а потом уже А • В + А • В. В таблице истинности появятся дополнительные столбцы для промежуточных результатов (рис. 3.7).
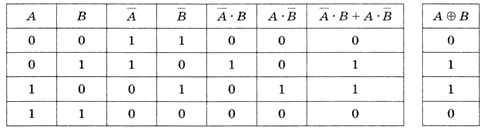
Рис. 3.7
Легко видеть, что выражение А • В + А • В совпадает с А ⊕ В для всех комбинаций значений. Это значит, что равенство доказано.
Операция «исключающее ИЛИ» иначе называется разделительной дизъюнкцией (это значит «один или другой, но не оба вместе») или сложением по модулю два. Второе название связано с тем, что её результат равен остатку от деления арифметической суммы А + В на 2:
А ⊕ В = (А + В) mod 2.
Здесь mod обозначает операцию взятия остатка от деления. Из таблицы истинности видно, что А ⊕ В = 1 тогда и только тогда, когда А ≠ В.
Операция «исключающее ИЛИ» обладает интересными свойствами. По таблице истинности несложно проверить, что
А ⊕ 0 = А, А ⊕ 1 = А, А ⊕ А = 0.
Для доказательства этих равенств можно просто подставить в них А = 0 и А = 1. Теперь докажем, что
(А ⊕ В) ⊕ В = А. (1)
Подставляя в левую часть В = 0, получим (А ⊕ 0) ⊕ 0 = А ⊕ 0 = А. Аналогично для В = 1 имеем (А ⊕ 1) ⊕ 1 = А ⊕ 1 = А. Это означает, что формула (1) справедлива для любых значений В. Отсюда следует важный вывод: если два раза применить операцию «исключающее ИЛИ» с одним и тем же значением переменной, мы восстановим исходное значение. В этом смысле «исключающее ИЛИ» — обратимая операция (кроме неё обратима также операция «НЕ» — если применить её дважды, мы вернёмся к исходному значению).
Формулу (1) можно использовать для шифрования данных. Пусть А и В — двоичные коды одинаковой длины. Чтобы зашифровать данные (А), используя ключ В, надо применить операцию «исключающее ИЛИ» отдельно для каждого разряда А и В. Для расшифровки ещё раз применяется «исключающее ИЛИ» с тем же ключом В. Нужно отметить, что такой метод шифрования очень нестойкий: для достаточно длинных текстов его легко «взломать» частотным анализом.
Следующая страница  Импликация
Импликация

