Урок 21
§17. Некоторые сведения из теории множеств

17.2. Операции над множествами

Над множествами, как и над числами, производят некоторые операции.

Пересечением двух множеств X и Y называется множество их общих элементов.

Пересечение множеств обозначают с помощью знака ∩: Х ∩ У. На рисунке 4.2 закрашено множество X ∩ Y.

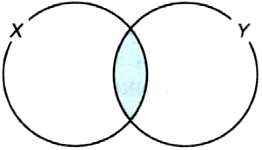
Рис. 4.2. Графическое изображение множества X ∩ Y

Пусть множества X и Y состоят из букв:

X = {ш к, о, л, а};

У = {у, р, о, к}.

Эти множества имеют общие элементы: к, о.

X ∩ У = { к, о}.

Множества М и X не имеют общих элементов, их пересечение — пустое множество:

М ∩ Х = ∅.

Пересечение множеств М и Р есть множество Р, а пересечение множеств М и М есть множество М:

М ∩ Р = Р;

М ∩ М = М.

Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.

Объединение множеств обозначают с помощью знака ∪: X ∪ У.

На рисунке 4.3 закрашено множество X ∪ У.

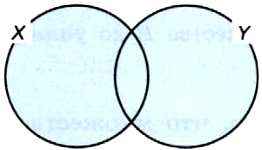
Рис. 4.3. Графическое изображение множества X ∪ У

Cкачать материалы урока