Урок 21
§17. Некоторые сведения из теории множеств

17.2. Операции над множествами (продолжение)

Для наших примеров:

Х ∪ У = {ш, к, о, л, а, у, р};

М ∪ X = {1, 3, 5, 7, 9, ш, к, о, л, а};

М ∪ Р = М; М ∪ М = М.

Подумайте, возможно ли равенство: А ∪ В = А ∩ В.

Пересечение и объединение выполняются для любой пары множеств. Третья операция — дополнение — имеет смысл не для всех множеств, а только тогда, когда второе множество является подмножеством первого.

Пусть множество Р является подмножеством множества М. Дополнением Р до М называется множество, состоящее из тех элементов М, которые не вошли в Р.

Дополнение Р до М обозначают 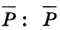= {7, 9}.

Дополнение М до М есть пустое множество, дополнение пустого множества до М есть .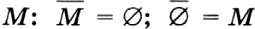

Особый интерес представляет дополнение некоторого множества В до универсального множества U. Например, если В — это множество точек, принадлежащих некоторому отрезку, то его дополнением 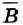до универсального множества U, которым в данном случае является множество всех точек числовой прямой, является множество точек, не принадлежащих данному отрезку.

В общем случае можем записать: 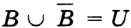(рис. 4.4)

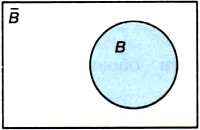
Рис. 4.4. Дополнение множества В до универсального множества

На рисунке 4.5 видно, что множество А ∪ В будет совпадать с универсальным, если А будет совпадать с множеством 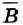или содержать его в качестве подмножества. В первом случае, т. е. при А = 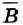, мы имеем дело с минимальным множеством А, таким что A ∪ В = U.

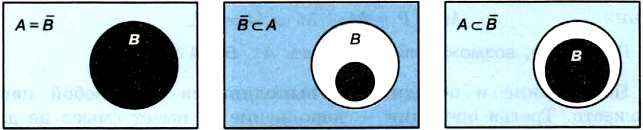
Рис. 4.5. Выбор такого множества А, что А ∪ В = U

Каким должно быть множество А для того, чтобы множество 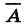∪ В совпадало с универсальным множеством?

Для ответа на этот вопрос воспользуйтесь рисунком 4.6.

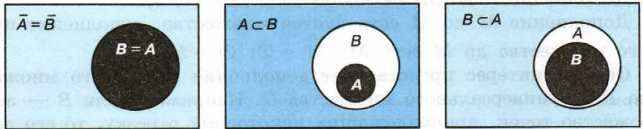
Рис. 4.6. Выбор такого множества А, что 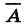∪  В = U

Cкачать материалы урока