Урок 21
§17. Некоторые сведения из теории множеств

17.3. Мощность множества

Мощностью конечного множества называется число его элементов.

Мощность множества X обозначается |Х|.

В рассмотренных выше примерах |Х| = 5, |М| = 5.

Число элементов объединения двух непересекающихся множеств равно сумме чисел элементов этих множеств. Так, в объединении множеств М и X содержится 10 элементов: |М ∪ Х| = 10.

Если же множества пересекаются, то число элементов объединения находится сложнее. Так, X состоит из 5 элементов, множество Y — из 4, а их объединение — из 7. Сложение чисел 5 и 4 даёт нам число 9. Но в эту сумму дважды вошло число элементов пересечения. Чтобы получить правильный результат, надо к числу элементов X прибавить число элементов Y и из суммы вычесть число элементов пересечения. Полученная формула подходит для любых двух множеств: |Х ∪ Y| = |Х| + |Y| — |Х ∩ Y|. Это частный случай так называемого принципа включений-исключений.

Принципом включений-исключений называется формула, позволяющая вычислить мощность объединения (пересечения) множеств, если известны их мощности и мощности всех их пересечений (объединений).

Для случая объединения трёх множеств формула имеет вид:

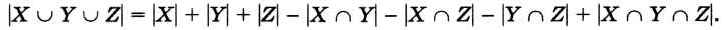
Аналогичные формулы справедливы и для пересечения множеств:

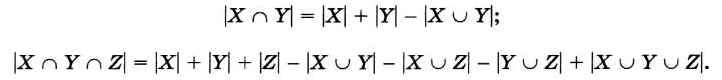
Пример. В зимний оздоровительный лагерь отправляется 100 старшеклассников. Почти все они увлекаются сноубордом, коньками или лыжами. При этом многие из них занимаются не одним, а двумя и даже тремя видами спорта. Организаторы выяснили, что всего кататься на сноуборде умеют 30 ребят, на лыжах — 28, на коньках — 42. Всего умением кататься на лыжах и сноуборде из них могут похвастаться 8 ребят, на лыжах и коньках — 10, на сноуборде и коньках — 5, но только трое из них владеют всеми тремя видами спорта.

Сколько ребят не умеет кататься ни на сноуборде, ни на лыжах, ни на коньках?

Обозначим через S, L и К множества сноуборд истов, лыжников и любителей коньков соответственно. Тогда |S| = 30, |L| = 28 и |К| = 42. При этом |S ∩ L| = 8, |К ∩ L| = 10, |S ∩ К| = 5, |S ∩ L ∩ K| = 3.

Объединение множеств S, L и К — это множество ребят, увлекающихся хотя бы каким-то видом спорта.

По формуле включений-исключений находим:

|S ∪ L ∪ К| = 30 + 28 + 42 - 8 - 10 - 5 + 3 = 80.

Таким образом, из 100 старшеклассников 20 не умеют кататься ни на сноуборде, ни на лыжах, ни на коньках.

Cкачать материалы урока