Уроки 63 - 73
§3.2. Алгебра логики
Содержание урока
3.2.1. Логическое умножение, сложение и отрицание
Логическое умножение (конъюнкция)
Логическое сложение (дизъюнкция)
Логическое отрицание (инверсия)
Практическое задание «Таблицы истинности»
Контрольные вопросы. Задания. Компьютерный практикум
3.2.2. Логические выражения
3.2.3. Логические функции
3.2.4. Логические законы и правила преобразования логических выражений
3.2.5. Решение логических задач
3.2.1. Логическое умножение, сложение и отрицание
Логическое сложение (дизъюнкция)
Объединение двух (или нескольких) высказываний с помощью союза «или» называется операцией логического сложения или дизъюнкцией.
Составное высказывание, образованное в результате логического сложения (дизъюнкции), истинно тогда и только тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Так, из приведенных ниже четырех составных высказываний, образованных с помощью операции логического сложения, ложно только первое, так как в последних трех составных высказываниях хотя бы одно из простых высказываний истинно:
1) «2 х 2 = 5 и 3 х 3 = 10»; 2) «2 х 2 = 5 и 3 х 3 = 9»; 3) «2 х 2 = 4 и 3 х 3 = 10»; 4) «2 х 2 = 4 и 3 х 3 = 9».
Запишем теперь операцию логического сложения на формальном языке алгебры логики. Операцию логического сложения (дизъюнкцию) принято обозначать значком «V». Операция логического сложения, аргументами которой являются логические переменные А и Б, записывается следующей формулой:
А ∨ В. (3.2)
Значение логической операции логического сложения задается с помощью таблицы истинности (табл. 3.2). Результатом операции логического сложения является «ложь» (0) тогда и только тогда, когда оба аргумента принимают значения «ложь» (0).
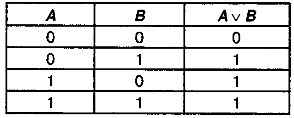
Таблица 3.2. Таблица истинности дизъюнкции (логического сложения)
По таблице истинности легко определить истинность составного высказывания, образованного с помощью операции логического сложения. Рассмотрим, например, составное высказывание «2 x 2 = 4 или 3 x 3 = 10». Первое простое высказывание истинно (А = 1), а второе высказывание ложно (В = 0), с помощью таблицы истинности логического сложения определяем, что данное составное высказывание истинно.
Следующая страница 
Логическое отрицание (инверсия)
Cкачать материалы урока
