Урок 27
Двоичная система счисления
Представление чисел в памяти компьютера

Правила двоичной арифметики гораздо проще правил десятичной арифметики. Вот все возможные варианты сложения и умножения однозначных двоичных чисел

Изучаемые вопросы:

- развернутая форма записи числа;
- перевод недесятичных чисел в десятичную систему счисления;
- перевод десятичных чисел в другие системы счисления;
- арифметика двоичных чисел.

Содержание урока

История чисел и систем счисления. Непозиционные системы древности

История чисел и систем счисления. Позиционные системы

История чисел и систем счисления. Вопросы и задания

Перевод чисел и двоичная арифметика

Перевод чисел и двоичная арифметика. Арифметика двоичных чисел

Перевод чисел и двоичная арифметика. Вопросы и задания

Перевод чисел и двоичная арифметика

Обсудим подробнее вопрос о представлении чисел в позиционных системах счисления, о правилах перевода чисел из одной позиционной системы счисления в другую.

Вспомним еще раз о том, что любое десятичное число можно пред ставить в виде суммы произведений значащих цифр числа на степени десятки. Такое представление называется развернутой формой записи числа. Посмотрите на следующие равенства:

2638 = 2 • 10000 + 6 • 100 + 3 • 10 + 8 =
= 2 • 10³ + 6 • 10² + 3 • 10¹ + 8 • 10⁰

345,178 = 3 • 100 + 4 • 10 + 5 + 1 • 0,1 + 7 • 0,01 + 8 • 0,001 =
= 3 • 10² + 4 • 10¹ + 5 • 10⁰ + 1 • 10^-1 + 7 • 10^-2 + 8 • 10^-3

Эти примеры показывают, что в развернутой форме показатель степени десяти зависит от позиции соответствующей цифры в записи числа. Позиция цифры в записи числа называется разрядом числа. Цифра в разряде единиц умножается на 10⁰ = 1; цифра в разряде десятков умножается на 10¹; цифра в разряде сотен — на 10² и т. д. Дробные разряды умножаются на отрицательные степени десяти: 10^-1, 10^-2, 10^-3 и т. д. Степень десятки равна номеру соответствующего разряда в числе (разряды дробной части нумеруются отрицательными числами).

Мы настолько привыкли к десятичному счету, что число в любой другой системе ничего нам не говорит о соответствующем ему количестве. Например, что за величина 112₃? Чтобы понять «много это или мало», нужно перевести его в десятичную систему. Сделать это довольно просто.

Число 112₃ содержит в себе 2 единицы, 1 тройку и 1 девятку. Как и в десятичной системе, число можно представить в виде суммы произведений составляющих его цифр и соответствующих степеней основания системы (в нашем примере — тройки).

112₃ = 1 • 3² + 1 • З¹ + 2 • 3⁰ = 9 + 3 + 2 = 14₁₀.

Следовательно, 112₃ = 14₁₀.

Переведем двоичное число 101101₂ в десятичную систему счисления. Принцип тот же. Теперь в развернутой форме числа надо использовать степени двойки:

101101₂ = 1 • 2⁵ + 0 • 2⁴ + 1 • 2³ + 1 • 2² + 0 • 2¹ + 1 • 2⁰ =
= 32 + 8 + 4 + 1 = 45₁₀

И еще один пример — с шестнадцатеричным числом:

15FC₁₆ = 1 • 16³ + 5 • 16² + 15 • 16¹ + 12 =
= 4096 + 1280 + 240 + 12 = 5628₁₀.

Аналогично переводятся дробные числа. Например:

101,11₂ = 1 • 2² + 0 • 2¹ + 1 • 2⁰ + 1 • 2^-1 + 1 • 2^-2 =
= 4 + 1 + 1/2 + 1/4 = 5 + 0,5 + 0,25 = 5,75₁₀.

А как произвести обратный перевод из десятичной системы в недесятичную (n + 10)? Для этого нужно суметь разложить десятичное число на слагаемые, содержащие степени n. Например:

15₁₀ = 8 + 4 + 2 + 1 = 1 • 2³ + 1 • 2² + 1 • 2¹ + 1 = 1111₂

Эта задача уже посложнее, чем перевод в десятичную систему. Попробуйте, например, таким образом перевести в двоичную систему число 157. Конечно, можно, но трудно!

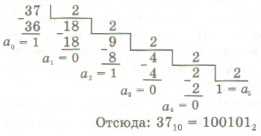
Однако существует формальная процедура, позволяющая легко выполнить такой перевод. Она состоит в том, что данное десятичное число делится с остатком на основание системы. Полученныи остаток — это младший разряд искомого числа, а полученное частное снова делится с остатком, который равен второй справа цифре и т. д. Так продолжается до тех пор, пока частное не станет меньше делителя (основания системы). Это частное — старшая цифра искомого числа.

Продемонстрируем этот метод на примере перевода числа 37₁₀ в двоичную систему. Здесь для обозначения цифр в записи числа используется символика:a₅a₄a₃a₂a₁a₀

Вот еще два примера перевода десятичного числа 315 в восьмеричную и шестнадцатеричную системы:

Отсюда следует: 315₁₀ = 473₈ = 13В₁₆. Напомним, что 11₁₀ = В₁₆.

Теперь рассмотрим перевод правильной десятичной дроби в другую систему счисления. Здесь работает следующее правило: перевод дробного десятичного числа в другую систему счисления производится путем последовательных умножений на основание новой системы с выделением цифр целой части произведений в качестве искомых.

Для примера покажем перевод десятичной дроби 0,1875 в двоичную, восьмеричную и шестнадцатеричную системы.

Здесь вертикальная черта отделяет целые части чисел от дробных частей. Подчеркиванием отмечены искомые значащие цифры дробного числа.

Отсюда: 0,1875₁₀ = 0,0011₂ = 014₈ = 0,3₁₆.

Умножение повторяется до тех пор, пока в дробной части очередного произведения не получится нуль, или не будет обнаружен период повторяющихся цифр.

При переводе дробного числа часто возникает ситуация, когда конечная дробь в десятичной системе переходит в бесконечную дробь (иррациональное число) в другой системе счисления. В таком случае, перед тем как производить перевод, нужно договориться о достаточной точности, т. е. о количестве знаков, которое сохраняется в дробной части числа.

Если число смешанное, т. е. имеется ненулевая целая и дробная части, то отдельно переводится его целая часть путем последовательного деления, отдельно — дробная путем умножения и затем оба результата записываются вместе через запятую. Из рассмотренных примеров следует:

315,1875₁₀ = 473,14₈ = 13В,3₁₆.