Уроки 27 - 30
Предикаты и кванторы. Логические элементы компьютера. Логические задачи
§23. Предикаты и кванторы. §24. Логические элементы компьютера. §25. Логические задачи
Содержание урока
§23. Предикаты и кванторы
Квантор
§24. Логические элементы компьютера
§25. Логические задачи
§23. Предикаты и кванторы
Квантор
Существуют предикаты, которые справедливы (истинны) для всех допустимых значений переменных. Например, это предикат Р(х) = (х2 ≥ 0), определённый на множестве всех вещественных чисел. В таком случае используют запись ∀хР(х), это означает: «При любом х предикат Р(х) справедлив». Знак ∀ — это буква «А», повёрнутая «вверх ногами» (от англ, all — все); он обозначает любой», «всякий», «для любого», «для всех». Символ ∀ называют квантором всеобщности.
Квантор (от лат. quantum — сколько) — это знак или выражение, обозначающее количество.
Выражения «любой», «для всех» и т. п. также можно считать кванторами, они равносильны знаку ∀.
Кванторы широко применяются в математике. Например, для натуральных п справедлива запись:
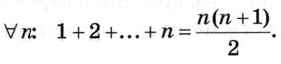
Часто используют ещё один квантор — квантор существования ∃ (зеркальное отражение буквы «Е», от англ, exist — существовать). Знак ∃ означает «существует», «хотя бы один». Например, если Р(х) = (х - 5 > 0), то можно записать ∃хР(х), что означает «Существует х, такой что х - 5 > 0». Это уже высказывание, а не предикат, потому что можно установить его истинность. Высказывание ∃хР(х) — истинно, так как существует х, удовлетворяющий данному условию, например х = 6. Запись ∀хР(х) — это тоже высказывание, но оно ложно, потому что неравенство х - 5 > 0 верно не для всех х.
Логическое выражение может включать несколько кванторов. Например, фразу «Для любого х существует у, такой что х + y = 0» можно записать как ∀x∃y(x + y = 0). Это утверждение истинно (на множестве чисел), потому что для любого х существует -х, число с обратным знаком. Переставлять местами кванторы нельзя, это меняет смысл выражения. Например, высказывание ∃ у ∀ х(х + y = 0) означает: «Существует такое значение y, что для любого х выполняется равенство х + y = 0», это ложное высказывание.
Теперь давайте вернёмся к Сократу, точнее, к двум высказываниям, приведённым в начале параграфа. Как записать утверждение «Все люди смертны»? Можно сказать иначе: «Для любого х верно: если х — человек, то х смертен». Вспоминаем, что связка «если..., то» записывается как импликация, а выражение «для любого х» — в виде квантора ∀ x.
Поэтому получаем:
∀x(P(x) → Q(x)),
где Р(х) = «х — человек», Q(x) = «х — смертен». Так как утверждение Р(х) → Q(x) верно для любого х, оно также верно при подстановке х = Сократ:
Р(Сократ) → Q(Сократ) = 1.
Поскольку Сократ — человек, то Р(Сократ) = 1. Поэтому с помощью таблицы истинности для импликации мы находим, что Q(Сократ) = 1, т. е. «Сократ смертен».
Если построить отрицание для высказывания с квантором ∀ или ∃, мы увидим, что один квантор заменяет другой. Например, отрицание высказывания ∀xP(x) («Неверно, что для любого х выполняется Р(х)») можно сформулировать так: «Существует хотя бы один х, для которого не выполняется Р(х)» и может быть записано в виде ∃хР(х). Здесь, как и раньше, черта сверху обозначает отрицание. Таким образом,
∀xP(x) = ∃хР(х).
Аналогично можно показать, что ∃хР(х) = ∀xP(x).
Где можно использовать язык предикатов? Самая подходящая для этого область информатики — системы искусственного интеллекта, в которых моделируется человеческое мышление. В таких системах часто применяется язык логического программирования Пролог, в котором программа представляет собой набор данных и правила вывода новых результатов из этих данных.
Следующая страница 
Подготовьте сообщение
Cкачать материалы урока
