Уроки 27 - 30
Предикаты и кванторы. Логические элементы компьютера. Логические задачи
§23. Предикаты и кванторы. §24. Логические элементы компьютера. §25. Логические задачи

Содержание урока

§23. Предикаты и кванторы

Предикат

Квантор

Подготовьте сообщение

Задачи

§24. Логические элементы компьютера

§25. Логические задачи

§23. Предикаты и кванторы

Задачи

1. Какие из следующих предложений являются предикатами (в заданиях а)-д) величины х и y — вещественные числа)?

а) х + у = 5;
б) ∃х(х + y = 5);
в) ∀у∃х(х + y = 5);
г) sin²х + cos²х = 1;
д) х² + y² < 0;
е) «х работает в вузе»;
ж) ∀x(«x — студент»);
з) ∃х(«х — учитель у»).

2. Задайте с помощью предикатов множества точек, соответствующие заштрихованным областям на плоскости:

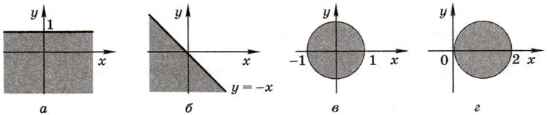
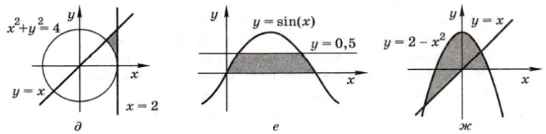
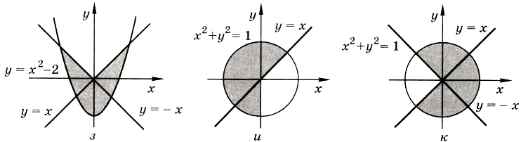
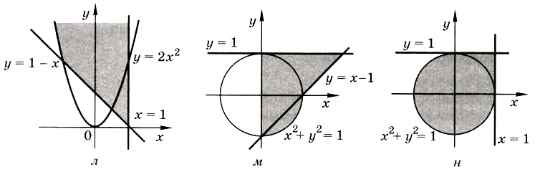
3. Поставьте в начале каждого предложения одно из слов: «все» или «не все».

а) «... окуни — рыбы».
б) «... рыбы умеют плавать».
в) «... реки впадают в моря».
г) «... моря солёные».
д) «... числа чётные».
е) «... ломаные состоят из отрезков».
ж) «... прямоугольники — квадраты».
з) «... кошки — млекопитающие».

4. Запишите с помощью кванторов следующие утверждения.

а) «Существует х, такой что х > y».
б) «Не существует х, такой что х > y».
в) «Для любого х имеем х² > 1».
г) «Любая река впадает в Каспийское море».
д) «Существует река, которая впадает в Каспийское море».
е) «Для любой реки существует море, в которое она впадает».
ж) «Для любого моря существует река, которая в него впадает».
з) «Существует река, которая впадает во все моря».
и) «Существует море, в которое впадают все реки».

*5. Запишите с помощью кванторов следующие утверждения:

а) «Некоторые школьники ходят в театр».
б) «Все кошки серые».
в) «Встречаются злые собаки».
г) «Все люди разные».
д) «Люди ошибаются».
е) «Никто не обращает на него внимания».
ж) «Ни одна фирма не обанкротилась».
з) «Все лебеди — белые или чёрные».

6. Запишите отрицание для следующих утверждений.

а) ∃х(х² = 5);
б) ∃х(х + y = 5);
в) ∀y(x + y = 5);
г) ∀y∃х(х + y = 5);
д) «х работает в вузе»;
е) ∀x(«х — студент»);
ж) ∃х(«х — учитель y»);
з) ∃х∀у(«х — учитель y»).

Следующая страница §24. Логические элементы компьютера

Cкачать материалы урока