Урок 31 - 35
Хранение в памяти целых и вещественных чисел. Арифметические и логические (битовые) операции. Маски
§26. Особенности представления чисел в компьютере. §27. Хранение в памяти целых чисел. § 28. Операции с целыми числами. §29. Хранение в памяти вещественных чисел
Содержание урока
§26. Особенности представления чисел в компьютере
§27. Хранение в памяти целых чисел
Целые числа без знака
§28. Операции с целыми числами
§29. Хранение в памяти вещественных чисел
§27. Хранение в памяти целых чисел
Целые числа без знака
Беззнаковые (англ, unsigned) типы данных, т. е. величины, не имеющие отрицательных значений, широко используются в вычислительной технике. Дело в том, что в задачах, решаемых на компьютерах, есть много таких значений: всевозможные счётчики (количество повторений циклов, число параметров в списке или символов в тексте), количество людей или предметов и др.
Чтобы закодировать целое число без знака, достаточно перевести его в двоичную систему счисления (см. § 11) и дополнить слева нулями до нужной разрядности. Например, число 28 записывается в 8-разрядную ячейку памяти так:
0001 1100
Это же число в 16-разрядном представлении будет иметь слева ещё 8 нулей. Восьмиразрядные коды некоторых характерных чисел приведены в табл. 4.1.
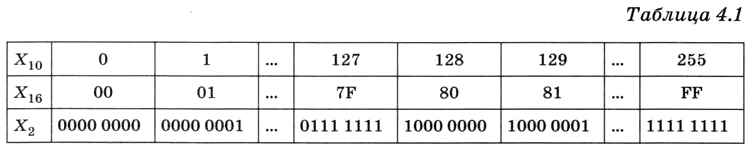
Минимальное значение для беззнаковых целых чисел всегда равно 0 (все разряды нулевые), а максимальное число Хmах = 2K - 1 состоит из всех единиц и определяется разрядностью (количеством битов) К (табл. 4.2).

Возникает вопрос: что будет, если увеличить максимальное число в К-битной ячейке на единицу? Рассмотрим случай К = 8 и попытаемся прибавить единицу к числу 25510 = 1111 11112. Добавляя дополнительный бит слева, получим:

Отбросив несуществующий дополнительный разряд 1, получаем 255 + 1 = 0. Как ни странно, именно это произойдёт в реальном компьютере. Говорят, что при К разрядах арифметика выполняется по модулю 2К, т. е. при К = 8 имеем 2:
(255 + 1) mod 256 = 256 mod 256 = 0.
1 На самом деле, для того чтобы обнаружить факт переполнения, этот разряд сохраняется в специальном управляющем бите процессора, который называется битом переноса.
2 Здесь запись a mod b обозначает остаток от деления а на b.
Вместе с тем, вычитая единицу из минимального значения 0, к которому добавлен старший разряд за пределами 8-битной ячейки, получим 1111 11112 = 25510 (проверьте это самостоятельно).
Можно заметить, что при многократном увеличении числа на единицу мы доходим до максимального значения и скачком возвращаемся к минимальному. При вычитании единицы получается обратная картина — дойдя до минимума (нуля), мы сразу перескакиваем на максимум (255). Поэтому для изображения допустимого диапазона чисел лучше подходит не отрезок числовой оси (как в математике), а окружность (рис. 4.6).
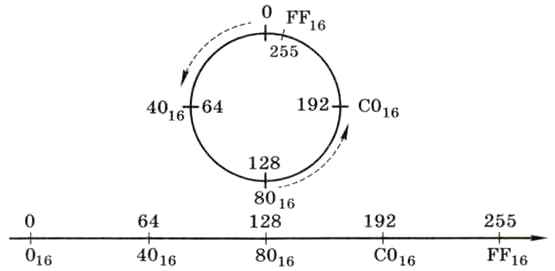
Рис. 4.6
Факт переполнения всегда фиксируется процессором, но выполнение программы не прерывается. Программе (точнее, программисту) предоставляется возможность как-то реагировать на переполнение или «не заметить» его.
Следующая страница  Целые числа со знаком
Целые числа со знаком

