Например, определим дополнительный код числа «-16», которое хранится в 8-разрядной ячейке. Здесь X = 16 = 10000₂. Используя алгоритмы А1 и А2, получаем:

Применение алгоритма А3 к числу 16 = 00010000₂ сводится к замене первых трёх нулей единицами: 1111 0000₂.

Для проверки можно сложить полученный результат с исходным числом и убедиться, что сумма обратится в ноль (перенос из старшего разряда не учитываем).

Повторное применение любого из алгоритмов А1 - А3 всегда приводит к восстановлению первоначального числа (убедитесь в этом самостоятельно). Это свойство также удобно использовать для проверки.

В таблице 4.3 показаны шестнадцатеричные и двоичные коды некоторых характерных 8-разрядных чисел.

Обратите внимание на скачок при переходе от -1 к 0 и на два граничных значения: 127 и «-128». «Кольцо» для чисел со знаком выглядит так, как показано на рис. 4.7.

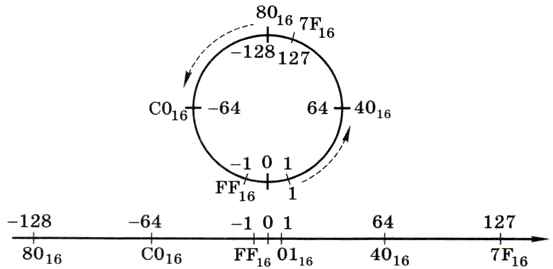
Рис. 4.7

Рис. 4.7

Чтобы сравнить коды целых чисел без знака и со знаком, объединим обе таблицы (4.1 и 4.3) — получим табл. 4.4.

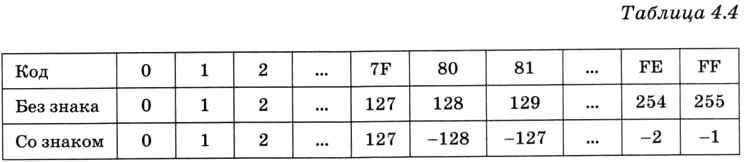
Общее количество значений со знаком и без знака одинаково, но их диапазоны сдвинуты друг относительно друга на числовой оси (рис. 4.8).

Рис. 4.8

Рис. 4.8

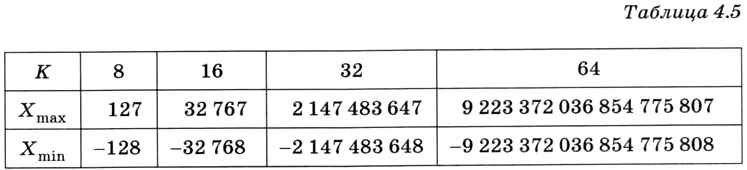
В наших рассуждениях использовались 8-разрядные числа, но все выводы справедливы для чисел любой разрядности. От числа разрядов К зависят только граничные значения Х_mах и X_min, приведённые в табл. 4.5.

Хотя дополнительный код гораздо менее нагляден, чем прямой, он значительно упрощает выполнение арифметических операций в компьютере. Например, вместо вычитания используется сложение с дополнительным кодом вычитаемого, поэтому не нужно проектировать специальное устройство для вычитания чисел.

Следующая страница Вопросы и задания

Cкачать материалы урока