Урок 31 - 35
Арифметические и логические (битовые) операции. Маски. Арифметические и логические (битовые) операции. Маски
§26. Особенности представления чисел в компьютере. §27. Хранение в памяти целых чисел. § 28. Операции с целыми числами. §29. Хранение в памяти вещественных чисел
Содержание урока
§26. Особенности представления чисел в компьютере
§27. Хранение в памяти целых чисел
§28. Операции с целыми числами
Сложение и вычитание
Поразрядные логические операции
§29. Хранение в памяти вещественных чисел
§28. Операции с целыми числами
Сложение и вычитание
Сложение и вычитание требуются не только для расчётов по формулам, но и для организации вычислений. Например, для того чтобы повторить какое-то действие R раз, используют переменную-счётчик, к которой после каждого выполнения этого действия прибавляют единицу, а затем результат сравнивают с R.
Вместо этого можно сразу записать в счётчик значение R и после каждого повторения вычитать из него единицу, пока не получится ноль 1.
1 Второй вариант более эффективен, потому что процессор автоматически сравнивает результат очередного действия с нулём.
Благодаря тому что отрицательные числа кодируются в дополнительном коде, при сложении можно не обращать внимания на знаки слагаемых, т. е. со знаковым разрядом обращаются точно так же, как и со всеми остальными.
Например, сложим числа 510 (0000 01012) и -910 (1111 01112), используя 8-разрядную двоичную арифметику. Применим сложение столбиком, не задумываясь о знаках чисел:

Для расшифровки получившегося отрицательного числа применим к нему схему получения дополнительного кода: 1111 1100 —< 0000 01002 = 410. Таким образом, результат равен -410, что совпадает с правилами «обычной» арифметики.
При сложении двух чисел с одинаковыми знаками может случиться переполнение — сумма будет содержать слишком большое количество разрядов. Покажем, как это выглядит для положительных и отрицательных чисел.
Сложим десятичные числа 96 и 33. Их сумма 129 выходит за 8-битную сетку. Для того чтобы обнаружить переполнение, добавим к обоим слагаемым ещё один старший бит, совпадающий со знаковым (рис. 4.9).

Рис. 4.9
Знаковый разряд S результата равен 1, т. е. сумма получилась отрицательной, хотя оба слагаемых положительны! Процессор определяет переполнение, сравнивая биты S и S': если они различны, то произошло переполнение и результат неверный (см. рис. 4.9).
То же самое получается, если сложить два достаточно больших по модулю отрицательных числа, например -96 и -33. Добавим к кодам обоих чисел один старший разряд, равный знаковому разряду (рис. 4.10).
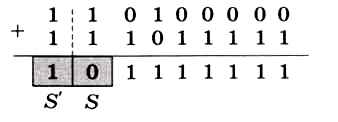
Рис. 4.10
Получается, что в результате бит S = 0, хотя ответ должен быть отрицательным. Биты S' и S не совпадают, это говорит о том, что произошло переполнение. Несложно проверить (сделайте это самостоятельно), что, если переполнения нет, значения битов S и S' всегда одинаковы независимо от знаков слагаемых.
Сложение многоразрядных двоичных чисел в компьютере выполняет специальное устройство — сумматор (см. главу 3). Как мы уже говорили, вычитание сводится к сложению с дополнительным кодом вычитаемого, поэтому отдельного «блока вычитания» в компьютере нет.
Следующая страница  Умножение и деление
Умножение и деление

