Урок 31 - 35
Арифметические и логические (битовые) операции. Маски. Арифметические и логические (битовые) операции. Маски
§26. Особенности представления чисел в компьютере. §27. Хранение в памяти целых чисел. § 28. Операции с целыми числами. §29. Хранение в памяти вещественных чисел
Содержание урока
§26. Особенности представления чисел в компьютере
§27. Хранение в памяти целых чисел
§28. Операции с целыми числами
Умножение и деление
Поразрядные логические операции
§29. Хранение в памяти вещественных чисел
§28. Операции с целыми числами
Умножение и деление
Умножение и деление выполнять труднее, чем сложение и вычитание. Вспомните, например, что в математике умножение часто заменяют многократным сложением, а деление — многократным вычитанием.
К двоичным числам можно применять обычную схему умножения «столбиком». Перемножим, например, числа 910 (0000 10012) и 510 (0000 01012):

Легко проверить, что это число равно 4510.
По сравнению с десятичной системой, здесь есть серьёзное упрощение: первый сомножитель умножается на единицу (в этом случае результат равен ему самому) или на ноль (результат — 0). Поэтому компьютерное умножение целых чисел состоит из следующих элементарных действий:
1) вычисление очередного произведения в зависимости от младшего бита второго сомножителя: оно равно нулю (если этот бит нулевой) или первому сомножителю (если бит равен единице);
2) сложение содержимого сумматора с очередным произведением;
3) сдвиг содержимого первого сомножителя влево на 1 разряд;
4) сдвиг второго сомножителя вправо на 1 разряд (при этом следующий бит попадёт в младший разряд).
Таким образом, удаётся построить схему умножения без использования таблицы умножения. Заметим, что умножение — это довольно трудоёмкая операция, и для её ускорения конструкторы используют различные «хитрые» приёмы. Поэтому в реальных компьютерах всё может выглядеть значительно сложнее, чем в учебном примере.
Умножение, как и сложение, выполняется одинаково для положительных и отрицательных чисел (в дополнительном коде). Если в нашем примере вместо числа 9 подставить -9, то получится:
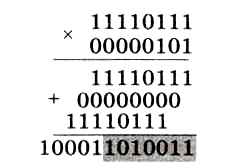
Оставив только 8 младших битов, можно убедиться (применяя алгоритмы А1-А3), что результат — это дополнительный код числа -45.
Теория деления нацело намного сложнее, чем приёмы умножения, поэтому мы её обсуждать не будем.
Следующая страница  Сравнение
Сравнение

