Урок 31 - 35
Арифметические и логические (битовые) операции. Маски. Арифметические и логические (битовые) операции. Маски
§26. Особенности представления чисел в компьютере. §27. Хранение в памяти целых чисел. § 28. Операции с целыми числами. §29. Хранение в памяти вещественных чисел
Содержание урока
§26. Особенности представления чисел в компьютере
§27. Хранение в памяти целых чисел
§28. Операции с целыми числами
Поразрядные логические операции
§29. Хранение в памяти вещественных чисел
§28. Операции с целыми числами
Поразрядные логические операции
В главе 3, изучая основы математической логики, мы увидели, что обработка истинности и ложности высказываний может быть представлена как набор операций с двоичными кодами. Оказывается, что логические операции, введённые первоначально для обработки логических данных, можно формально применить к битам двоичного числа, и такой подход широко используется в современных компьютерах.
Рассмотрим электронное устройство для управления гирляндой лампочек. Состояние каждой лампочки будет задаваться отдельным битом в некотором управляющем регистре: если бит равен нулю, лампочка выключена, если единице — включена. Для получения различных световых эффектов (типа «бегущих огней») требуется зажигать или гасить отдельные лампочки, менять их состояние на противоположное и т. д. (рис. 4.11). Точно так же биты регистров используются для управления внешними устройствами.
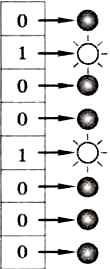
Рис. 4.11
Будем применять логические операции к каждому биту числа, как обычно, считая, что 1 соответствует значению «истина», а 0 — «ложь». Эти операции часто называют поразрядными или битовыми, поскольку действия совершаются над каждым разрядом в отдельности, независимо друг от друга 1.
Введём несколько терминов, которые используются в литературе по вычислительной технике. Сброс — это запись в бит нулевого значения, а установка — запись единицы. Таким образом, если бит в результате какой-то операции становится равным нулю, то говорят, что он сбрасывается. Аналогично, когда в него записана единица, говорят, что бит установлен.
Маска — это константа (постоянная), которая определяет область применения логической операции к битам многоразрядного числа. С помощью маски можно скрывать (защищать) или открывать для выполнения операции отдельные биты 2.
1 Для сравнения, сложение (как и другие арифметические действия) не является поразрядной операцией, поскольку возможен перенос из младшего разряда в старший.
2 Использование маски аналогично выделению области рисунка в графическом редакторе — для выделенных пикселей маска равна 1, для остальных — нулю.
Основные логические операции в современных процессорах — это «НЕ» (not), «И» (and), «ИЛИ» (or) и «исключающее ИЛИ» (хог).
Логическое «НЕ» (инвертирование, инверсия, not) — это замена всех битов числа на обратные значения: 0 на 1, а 1 — на 0. Эта операция используется, например, для получения дополнительного кода отрицательных чисел (см. алгоритм А1 в § 27). «НЕ» — это унарная операция, т. е. она действует на все биты одного числа. Маска здесь не используется.
Логическое «И» (and). Обозначим через D содержимое некоторого бита данных, а через М — значение соответствующего ему бита маски. Операция «И» между ними задаётся таблицей, показанной на рис. 4.12.
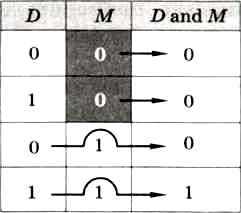
Рис. 4.12
Из таблицы видно, что при выполнении логического «И» нулевой бит в маске всегда сбрасывает (делает равным нулю) соответствующий бит результата, а единичный бит позволяет сохранить значение D (как бы пропускает его, открывая «окошко»).
С помощью логической операции «И» можно сбросить отдельные биты числа (те, для которых маска нулевая), не меняя значения остальных битов (для которых в маске стоят единицы).
Например, операция X and 1 сбросит у любого числа X все биты, кроме самого младшего. С помощью этого приёма легко узнать, является ли число чётным: остаток от деления на 2 равен последнему биту!
Логическое «ИЛИ». Вспомнив таблицу истинности логической операции «ИЛИ» (or), можно обнаружить, что в ноль в маске сохраняет бит (X or 0 = X), а единица устанавливает соответствующий бит результата (X or 1 = 1) (рис. 4.13).
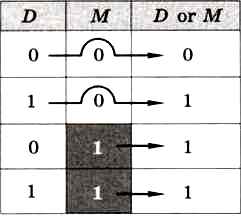
Рис. 4.13
С помощью логической операции «ИЛИ» можно установить отдельные биты числа (те, для которых маска единичная), не меняя значения остальных битов (для которых в маске стоят нули).
Например, операция X or 8016 установит старший бит восьмиразрядного числа X, формально сделав тем самым число отрицательным.
Таким образом, используя операции «И» и «ИЛИ», можно сбрасывать и устанавливать любые биты числа, т. е. строить любой нужный двоичный код. Где это может пригодиться? Рассмотрим примеры решения конкретных задач.
Пример 1. На клавиатуре набраны 3 цифры, образующие значение целого числа без знака. Определить, какое число было введено.
При нажатии клавиши на клавиатуре в компьютер поступает код нажатой клавиши. Выпишем десятичные и шестнадцатеричные коды всех символов, обозначающих цифры:
Будем пользоваться шестнадцатеричными кодами: как видно из таблицы, их связь с цифрами числа гораздо нагляднее. Чтобы получить числовое значение цифры из кода символа X, достаточно сбросить его старшие четыре бита, не изменяя значений четырёх младших битов. Для этого нужно использовать операцию X and 0F16.
Пусть S1 — код первого введённого символа, S2 — второго, S3 — третьего, а N обозначает искомое число. Тогда алгоритм перевода кодов символов в число выглядит так:
1. N = 0.
2. W = S1 and 0F16 (выделяем первую цифру).
3. N = 10 • N + W (добавляем её к числу).
4. W = S2 and 0F16 (выделяем вторую цифру).
5. N = 10 • N + W (добавляем её к числу).
6. W = S3 and 0F16 (выделяем третью цифру).
7. N = 10 • N + W (добавляем её к числу).
Пусть, например, набраны символы '1', '2' и '3'. Тогда по таблице находим, что S1 =3116, S2 = 3216 и S3 =3316. Значение W на втором шаге вычисляется так:
Так как W = 1, на третьем шаге получаем N = 1. Следующая пара шагов — четвёртый и пятый — дают результаты W = 2 и N = 12 соответственно. Наконец, результат завершающих шагов: W = 3 и N = 123.
Такая процедура используется в каждом компьютере: именно так коды цифровых символов, набранные на клавиатуре, преобразуются в числа, с которыми компьютер выполняет арифметические действия. Заметим, что фактически здесь использована схема Горнера для представления целого числа (см. § 10).
Пример 2. Создадим структуру данных S, которая отражает, есть или нет в некотором числе каждая из цифр от 0 до 9. В математике такая структура называется множеством.
Для хранения S будем использовать 16-разрядное целое число (рис. 4.14).
Рис. 4.14
Договоримся, что младший бит числа имеет номер 0 и хранит информацию о том, есть во множестве цифра 0 (если этот бит равен 0, такой цифры нет, если равен 1, то есть). Аналогично первый бит (второй по счёту справа) показывает, есть ли во множестве цифра 1, и т. д. Старшие биты 10-15 при этом не используются. Например, во множестве, изображенном на рис. 4.14, есть только цифры 0, 3, 6 и 9.
Для записи элементов во множество и проверки их наличия удобно использовать логические операции. Рассмотрим для примера бит 5. Маска, которая потребуется для обращения к нему, — это единица в пятом разряде и нули во всех остальных, т. е. М = 002016. С её помощью можно добавить элемент к множеству с помощью операции «ИЛИ»: S = S or М. А узнать, есть ли во множестве интересующая нас цифра, можно, выделив соответствующий бит с помощью логического «И» (Р = S and М) и проверив результат на равенство нулю.
Исключающее ИЛИ. Как видно из таблицы истинности, операция «исключающее ИЛИ» (хог) не изменяет биты, когда маска нулевая, и меняет биты на противоположные при единичной маске (рис. 4.15).
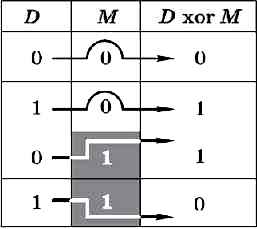
Рис. 4.15
Например, команда Y = Y хоr FF16 выполняет инверсию всех битов 8-разрядного целого числа. Напомним, что это один из этапов получения дополнительного кода отрицательных чисел.
С помощью логической операции «исключающее ИЛИ» можно выполнить инверсию отдельных битов числа (тех, для которых маска единичная), не меняя значения остальных битов (для которых в маске стоят нули).
Пример 3. Пусть X — это результат выполнения некоторого вычислительного теста, а Y — то, что ожидалось получить («правильное» значение). Нужно определить, в каких разрядах различаются эти числа (для инженера это очень полезная подсказка, где искать неисправность).
Предположим, что Х = 7, Y = 3. В результате операции X хоr У устанавливаются (в единицу) только те разряды, которые в этих числах не совпали, а остальные сбрасываются 3. В данном случае находим, что числа различаются только одним битом:
3 Профессиональные программисты часто используют операцию хоr для обнуления переменной: команда R := R хоr R запишет в переменную R ноль, независимо от её начального значения.
Пример 4. Используя логическую операцию «исключающее ИЛИ», можно шифровать любые данные. Покажем это на примере простого текста '2*2=4'.
Выберем любую маску, например 2310 = 0001 01112. Эта маска представляет собой ключ шифра — зная ключ, можно расшифровать сообщение. Возьмём первый символ — цифру '2', которая имеет код 5010 = ООН 00102, и применим операцию «исключающее ИЛИ» с выбранной маской:
Полученное значение 0010 01012 = 3710 — это код символа '%’. Для расшифровки применим к этому коду «исключающее ИЛИ» с той же маской:
В результате получили число 50 — код исходной цифры '2'.
Повторное применение операции «исключающее ИЛИ» с той же маской восстанавливает исходное значение, т. е. эта логическая операция обратима.
Если применить такую процедуру шифрования ко всем символам текста '2*2=4', то получится зашифрованный текст '%=%*#'.
Обратимость операции «исключающее ИЛИ» часто используется в компьютерной графике для временного наложения одного изображения на другое. Это может потребоваться, например, для выделения области с помощью инвертирования её цвета.
Следующая страница 
Сдвиги
Cкачать материалы урока
