Урок 31 - 35
Арифметические и логические (битовые) операции. Маски. Арифметические и логические (битовые) операции. Маски
§26. Особенности представления чисел в компьютере. §27. Хранение в памяти целых чисел. § 28. Операции с целыми числами. §29. Хранение в памяти вещественных чисел
Содержание урока
§26. Особенности представления чисел в компьютере
§27. Хранение в памяти целых чисел
§28. Операции с целыми числами
Поразрядные логические операции
Сдвиги
§29. Хранение в памяти вещественных чисел
§28. Операции с целыми числами
Сдвиги
Об операции сдвига вспоминают гораздо реже, чем она того заслуживает. Перечитайте ещё раз алгоритм умножения, описанный выше, и вы убедитесь, что он весь построен на сдвигах. Сдвиги незаменимы тогда, когда требуется проделать ту или иную обработку каждого бита, входящего в число. Наконец, сдвиги двоичного числа позволяют быстро умножить или разделить число на степени двойки: 2, 4, 8 и т. д. Поэтому программисты очень ценят и широко применяют всевозможные разновидности сдвигов.
Идея операции сдвига довольно проста: все биты кода одновременно сдвигаются в соседние разряды 1 влево или вправо (рис. 4.16).
1 Аппаратно сдвиг реализуется необычайно просто и изящно: регистр, содержащий число, сбрасывается в ноль, при этом из тех разрядов, где исчезла единица, электрический импульс проходит в соседние и устанавливает их в единицу. При этом важно, что все разряды обрабатываются одновременно.
Рис. 4.16
Отдельно надо поговорить о двух крайних битах, у которых «нет соседей». Для определённости обсудим сдвиг влево. Для самого младшего бита (на рис. 4.16 он крайний справа) данные взять неоткуда, поэтому в него просто заносится ноль. Самый старший (крайний слева) бит должен потеряться, так как его некуда сохранить. Чтобы данные не пропали, содержимое этого разряда копируется в специальную ячейку процессора — бит переноса 2 С (от англ, carry — перенос), с которым может работать процессор.
2 При программировании на языках высокого уровня бит переноса недоступен.
Рассмотренный тип сдвига обычно называется логическим сдвигом. Его можно использовать для быстрого умножения и деления. Рассмотрим, например, 8-разрядный двоичный код 0000 1100, который представляет число 1210. Выполнив логический сдвиг влево, получим 0001 1000, т. е. число 2410, которое вдвое больше! Это не случайность: вспомните, что происходит, если к десятичному числу справа приписать дополнительный ноль, например 34 -> 340.
При сдвиге вправо любое чётное число уменьшается ровно в 2 раза. В случае нечётного значения происходит деление нацело, при котором остаток отбрасывается. Например, из 0001 0001 = 1710 при сдвиге вправо получается 0000 1000 = 810.
Логический сдвиг влево на 1 разряд увеличивает целое положительное число вдвое, а сдвиг вправо делит на 2 нацело.
Пример. Для умножения числа, находящегося в ячейке Z, на 10 можно использовать такой алгоритм:
1. Сдвиг влево Z (в ячейке Z получаем 2Z0, где Z0 — исходное число).
2. X = Z (сохраним 2Z0).
3. Сдвиг на 2 бита влево X (вычислили 8Z0).
4. X = X + Z (X = 8Z0 + 2Z0 = 10Z0).
Для некоторых компьютеров такая последовательность выполняется быстрее, чем стандартная операция умножения.
Посмотрим, что получится для отрицательных чисел. Сдвинем влево код 1111 1000 (8-разрядное представление числа —8):
получится 1111 0000. Легко проверить, что это дополнительный код числа -16, т. е. значение удвоилось! Но со сдвигом вправо ничего не получается: из 1111 1000 получаем 0111 1100 — это код положительного числа! Дело в том, что при сдвиге вправо отрицательных чисел, в отличие от положительных, старший разряд надо заполнять не нулём, а единицей! Чтобы исправить положение, вводится ещё одна разновидность сдвига — арифметический сдвиг. Его единственное отличие от логического состоит в том, что старший (знаковый) бит не меняется, т. е. знак числа остаётся прежним (рис. 4.17).
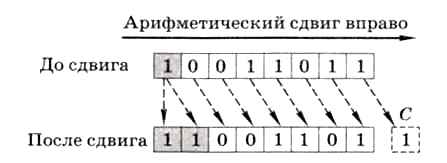
Рис. 4.17
Если применить арифметический сдвиг к коду 1111 1000, получается 1111 1100 — дополнительный код числа -4, т. е. произошло деление на 2. В качестве упражнения проверьте, как ведёт себя отрицательное нечётное число при арифметическом сдвиге вправо.
Арифметический сдвиг влево не требуется, поскольку он ничем не отличается от обычного логического сдвига.
То, что в результате логических сдвигов содержимое крайних разрядов теряется, не всегда удобно. Поэтому в компьютере предусмотрен циклический сдвиг, при котором бит из одного крайнего разряда переносится в другой («по циклу», рис. 4.18).
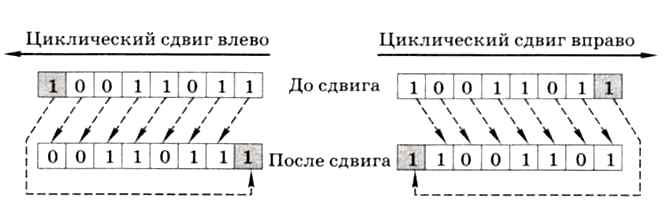
Рис. 4.18
Циклический сдвиг позволяет «просмотреть» все биты и вернуться к исходному значению. Если сделать последовательно 8 циклических сдвигов 8-битного числа, каждый его бит на каком-то шаге окажется на месте младшего разряда, где его можно выделить с помощью логической операции «И» с маской 1. Так можно «просматривать» не только младший, но и любой другой разряд (например, для выделения старшего разряда нужно использовать маску 8016).
Следующая страница 
Вопросы и задания
Cкачать материалы урока
