Урок 119
Модификаторы
(§69. Модификаторы)

Содержание урока

Что это такое?

Сглаживание

Симметрия

Логические операции

Массив

Деформация

Вопросы и задания

Задачи

Логические операции

С помощью модификатора Логический (англ. boolean) можно строить объединение, пересечение и «разность» двух объектов. На рисунке 9.21 показаны четыре возможные «логические» операции, которые можно применить к кубу и сфере.

Рис. 9.21

Легко заметить, что объединение и пересечение можно сопоставить логическим операциям «ИЛИ» и «И», которые вы изучали в 10 классе.

Модификатор применяется к одному объекту, а второй указывается в параметрах модификатора в поле Объект (Object). На рисунке 9.22 показаны настройки модификатора Логический для случая, когда нужно построить «разность» сферы (объект с именем Sphere) и куба (объект Cube). Список Операция (Operation) позволяет выбрать нужную операцию (здесь — операция Разность (Difference)). При этом куб никак не меняется, а вместо сферы, к которой применён модификатор, появляется объект «сфера минус куб», т. е. часть шара, которая не входит в куб.

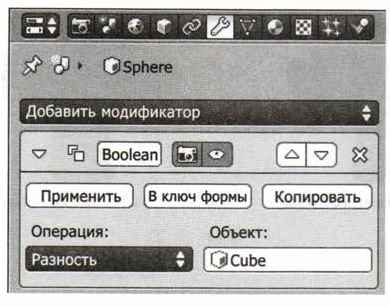
Рис. 9.22

Если после этого сдвинуть куб, полученный объект-«разность» изменится, потому что он каждый раз строится заново с учётом текущего положения сферы и куба. Чтобы новый объект стал независимым, нужно применить модификатор с помощью кнопки Применить (Apply). Теперь изменения куба не будут на него влиять.

Сетка объекта, полученного в результате логической операции, значительно усложняется в местах стыковки исходных тел, поэтому потом её довольно сложно редактировать.

Следующая страница Массив

Cкачать материалы урока