Урок 16
§2.2.Кодирование и обработка графической информации
§2.2.3. Векторная графика. Практическая работа 2.7. Работа с трёхмерной векторной графикой. Практическая работа 2.8. Выполнение геометрических построений в системе компьютерного черчения КОМПАС
Содержание урока
Практическая работа 2.7. Работа с трёхмерной векторной графикой
Практическая работа 2.8.1. Геометрическое построение угла, равного заданному
Практическая работа 2.8.2. Построение треугольника по двум сторонам и углу между ними
Практическая работа 2.8.3. Построение треугольника по трём сторонам
Практическая работа 2.8.4. Построение перпендикуляра к заданной прямой
Практическая работа 2.8.5. Построение биссектрисы неразвёрнутого угла
Практическая работа 2.8.1
Геометрическое построение угла, равного заданному
Электронное приложение к главе 2.
Формальная модель. Построим формальную модель процесса геометрического построения, зафиксировав его в форме алгоритма:
1. Построить угол А и луч ОМ.
2. Построить окружность произвольного радиуса с центром в точке А, обозначить точки пересечения окружности со сторонами угла буквами В и С.
3. Построить окружность такого же радиуса с центром в точке О, обозначить точку пересечения окружности с лучом ОМ буквой D.
4. Построить окружность с радиусом, равным отрезку ВС с центром в точке D, обозначить точку пересечения окружностей буквой Е.
5. Соединить отрезком точки О и В. Угол EOD, равный углу А, построен.
Начертим геометрические объекты, заданные в условии задачи: произвольный угол и отрезок.
1. С помощью Компактной панели вызвать панель Геометрия. Выбрать объект Отрезок и построить сначала произвольный угол А (начертить два отрезка, выходящих из одной точки), а затем построить произвольный луч ОМ (начертить отрезок).
Введём обозначение точек на чертеже с помощью панели Обозначения.
2. С помощью Компактной панели вызвать панель Обозначения. Щёлкнуть по кнопке Ввод текста и последовательно ввести обозначения угла и концов отрезка (рис. 2.37).
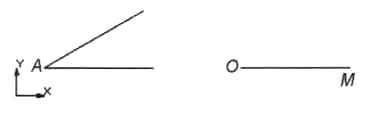
Рис. 2.37
Построим окружность произвольного радиуса с центром в вершине заданного угла А, которая пересечёт стороны угла в точках В и С.
3. На панели Геометрия выбрать объект Окружность и построить окружность с центром в точке А.
На панели Обозначения щёлкнуть по кнопке Ввод текста и обозначить точки пересечения окружности со сторонами угла буквами Б и С (рис. 2.38).
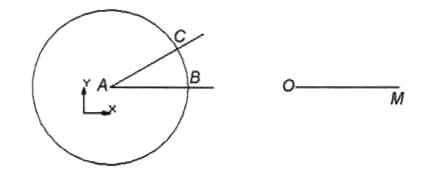
Рис. 2.38
Построим окружность того же радиуса с центром в начале заданного луча ОМ, которая пересечёт отрезок ОМ в точке D.
4. На панели Геометрия выбрать объект Окружность.
На Панели свойств (рис. 2.39) щёлкнуть правой кнопкой мыши по полю
Радиус и в контекстном меню выбрать пункт Между 2 точками.
На чертеже навести курсор сначала на точку А, а затем на точку В.
Центр появившейся окружности заданного радиуса переместить в точку О.
Рис. 2.39
5. На панели Обозначения щёлкнуть по кнопке Ввод текста и обозначить точку пересечения окружности с отрезком ОМ буквой D (рис. 2.40).
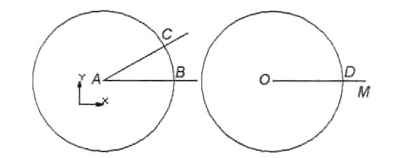
Рис. 2.40
Построим окружность с центром в точке D заданного радиуса ВС.
6. На панели Геометрия выбрать объект Окружность.
На Панели свойств щёлкнуть правой кнопкой мыши по полю Радиус и в контекстном меню выбрать пункт Между 2 точками.
На чертеже навести курсор сначала на точку С, а затем на точку В.
Центр появившейся окружности заданного радиуса переместить в точку D.
7. На панели Обозначения щёлкнуть по кнопке Ввод текста и обозначить точку пересечения окружностей буквой Е.
8. Соединить отрезком точки О и Е. Угол EOD, равный углу А, построен (рис. 2.41).
Рис. 2.41
Следующая страница 
Практическая работа 2.8.2. Построение треугольника по двум сторонам и углу между ними
Cкачать материалы урока
